
【题目】如图,已知二次函数![]() (a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④
(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点B在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0;②4a+2b+c>0;③4ac-b2<16a;④![]() <a<
<a<![]() ;⑤b>c.其中正确结论个数( )
;⑤b>c.其中正确结论个数( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】试题解析:①∵函数开口方向向上,∴a>0;
∵对称轴在y轴右侧,
∴ab异号,
∵抛物线与y轴交点在y轴负半轴,
∴c<0,
∴abc>0,
故①正确;
②∵图象与x轴交于点A(1,0),对称轴为直线x=1,
∴图象与x轴的另一个交点为(3,0),
∴当x=2时,y<0,
∴4a+2b+c<0,
故②错误;
③∵图象与x轴交于点A(1,0),
∴当x=1时, ![]()
∴ab+c=0,即a=bc,c=ba,
∵对称轴为直线x=1
![]() 即b=2a,
即b=2a,
∴c=ba=(2a)a=3a,
![]()
![]()
![]() 故③正确.
故③正确.
④∵图象与y轴的交点B在(0,2)和(0,1)之间,
∴2<c<1
∴2<3a<1,
![]()
故④正确.
⑤∵a>0,
∴bc>0,即b>c;
故⑤正确;
故选C.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
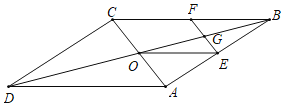
(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是![]() .
.
(1)求暗箱中红球的个数;
(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是______________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系: .
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系: . (3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
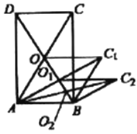
【题目】如图,矩形![]() 的面积为20,对角线
的面积为20,对角线![]() ,
,![]() 交于点
交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.45
D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若BD=3,CE=2,求△ABC的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,按选做的第一题计分.
A:如图1,AD是正五边形ABCDE的一条对角线,则∠BAD= .
B:如图2,小明从坡角为27.5°的斜坡的坡底A走到离A水平距离10米远(AC=10米)的C处,则他走过的坡面距离AB为 米(结果精确到0.01米)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com