
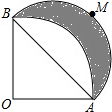
 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.  经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
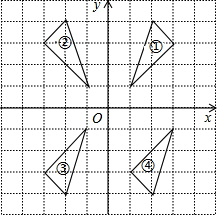 如图所示,编号为①②③④的四个三角形
如图所示,编号为①②③④的四个三角形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
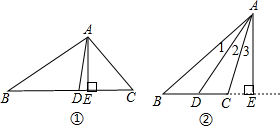 求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.
求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
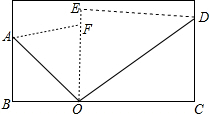 将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.
将一张矩形纸片按如图方式折叠,设O点是矩形边上一点,将矩形的一角沿OA翻折使OB与OF重合,再将其邻角沿0D翻折,使OC与OE重合,且O、E、F在同一直线上.求OA与∠BOF、OD与∠EOC的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
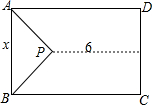 如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
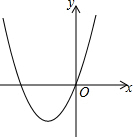 已知抛物线的顶点为(-2,-3),且经过原点,
已知抛物线的顶点为(-2,-3),且经过原点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
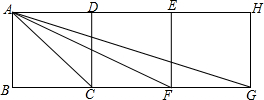 如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG
如图,四边形ABCD,CDEF,EFGH均是正方形,且B,C,F,G在一直线上,连接AC,AF,AG查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com