
 如图,将边长为2a(a>0)的正方形ABCD折叠,使顶点A与CD边上的点M重合,折线交AD于E,交BC于F,边AB折叠后与BC交于点G.
如图,将边长为2a(a>0)的正方形ABCD折叠,使顶点A与CD边上的点M重合,折线交AD于E,交BC于F,边AB折叠后与BC交于点G.分析 (1)设DE为x,则根据折叠知道DM=a,EM=EA=2a-x,然后在Rt△DEM中就可以求出x,可得出DE,DN,EM的长,从而求出它们的比值;
(2)△CMG的周长与点M的位置无关.设DM=x,DE=y,则CM=2a-x,EM=2a-y,然后利用正方形的性质和折叠可以证明△DEM∽△CMG,利用相似三角形的对应边成比例可以把CG,MG分别用x,y分别表示,△CMG的周长也用x,y表示,然后在Rt△DEM中根据勾股定理可以得到4a2-x2=4ay,结合△CMG的周长,就可以判断△CMG的周长与点M的位置无关.
解答 证明:(1)DE为x,则DM=a,EM=EA=2a-x,
在Rt△DEM中,∠D=90°,
∴DE2+DM2=EM2
x2+a2=(2-a)2
x=$\frac{3}{4}$a,
∴EM=$\frac{5}{4}$a.
∴DE:DM:EM=3:4:5;
(3)△CMG的周长与点M的位置无关.
证明:设DM=x,DE=y,则CM=2a-x,EM=2a-y,
∵∠EMG=90°,
∴∠DME+∠CMG=90°.
∵∠DME+∠DEM=90°,
∴∠DEM=∠CMG,
又∵∠D=∠C=90°,
∴△DEM∽△CMG,
∴$\frac{CG}{DM}$=$\frac{CM}{DE}$=$\frac{MG}{EM}$即$\frac{CG}{x}$=$\frac{2a-x}{y}$=$\frac{MG}{2a-y}$,
∴CG=$\frac{x(2a-x)}{y}$,MG=$\frac{(2a-x)(2a-y)}{y}$,
∴△CMG的周长为CM+CG+MG=$\frac{4{a}^{2}-{x}^{2}}{y}$,
∵在Rt△DEM中,DM2+DE2=EM2
∴x2+y2=(2a-y)2
整理得4a2-x2=4ay,
∴CM+MG+CG=$\frac{4ay}{y}$=4a.
所以△CMG,的周长为4a,与点M的位置无关.
点评 本题考查的是翻折变换的性质、相似三角形的应用和正方形性质的应用,正方形的有些题目有时用代数的计算证明比用几何方法简单,甚至几何方法不能解决的用代数方法可以解决,属于中考常考题型.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题
 如图,A,F,E,B四点在同一直线上,AC⊥CE,BD⊥DF,AF=BE,AC=BD.试判断DF与CE的关系(指数量与位置关系),并说明理由.
如图,A,F,E,B四点在同一直线上,AC⊥CE,BD⊥DF,AF=BE,AC=BD.试判断DF与CE的关系(指数量与位置关系),并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?
如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
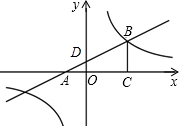 如图,平面直角坐标系中,直线y=$\frac{1}{2}$x+$\frac{1}{2}$与x轴交于点A,与y轴交于点D,与双曲线y=$\frac{k}{x}$在第一象限内交于点B,BC⊥x轴于点C,AB=3AD.求双曲线的解析式.
如图,平面直角坐标系中,直线y=$\frac{1}{2}$x+$\frac{1}{2}$与x轴交于点A,与y轴交于点D,与双曲线y=$\frac{k}{x}$在第一象限内交于点B,BC⊥x轴于点C,AB=3AD.求双曲线的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com