
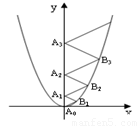
二次函数 的图象如图所示,点
的图象如图所示,点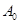 位于坐标原点, 点
位于坐标原点, 点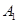 ,
, ,
, ,…,
,…,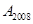 在y轴的正半轴上,点
在y轴的正半轴上,点 ,
, ,
, ,…,
,…,  在二次函数
在二次函数 位于第一象限的图象上, 若△
位于第一象限的图象上, 若△ ,△
,△ ,△
,△ ,…,△
,…,△ 都为等边三角形,则△
都为等边三角形,则△ 的边长=
的边长=
2008
【解析】本题考查了二次函数的综合.
此题需要从简单的例子入手寻找各三角形边长的规律;可设出△A0A1B1的边长为m1,由于此三角形是正三角形,则∠B1A0A1=60°,∠B1A0x=30°,可用边长m1表示出B1的坐标,代入抛物线的解析式中,即可得到m1的值,同理可求出△A1B2A2、△A2B3A3的边长,通过观察得到这些三角形边长值的变化规律来求得到△A2008B2009A2009的边长
解:设△A0A1B1的边长为m1;
∵△A0A1B1是等边三角形,
∴∠A1A0B1=60°,∠B1A0x=30°;
故B1(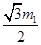 ,
,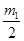 )
)
由于点B1在抛物线的图象上,则有:
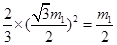
解得m1=1;
同理设△A1A2B2的边长为m2
同上可得B2( ,
,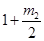 );
);
由于点B2也在抛物线的图象上,则有:

解得m2=2;
依此类推,△A2B3A3的边长为:m3=3,
…
△AnBn+1An+1的边长为mn+1=n+1;
∴△A2007B2008A2008的边长为2008.


科目:初中数学 来源: 题型:
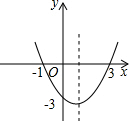 已知二次函数的图象如图所示,则这个二次函数的表达式为( )
已知二次函数的图象如图所示,则这个二次函数的表达式为( )| A、y=x2-2x+3 | B、y=x2-2x-3 | C、y=x2+2x-3 | D、y=x2+2x+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 16、已知二次函数的图象如图所示,则
16、已知二次函数的图象如图所示,则查看答案和解析>>
科目:初中数学 来源: 题型:
 二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点.
二次函数的图象如图所示,P为图象顶点,A为图象与y轴交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com