
分析 (Ⅰ)分别利用乘车收费标准求出不同路程的乘车费用;
(Ⅱ)利用某人乘坐了x(x>5且为整数)千米的路程,进而利用乘车收费标准得出答案;
(Ⅲ)首先求出此人乘车的路程超过5千米,进而利用(Ⅱ)所求得出等式求出答案.
解答 解:(Ⅰ)由题意可得:某人乘坐了2千米的路程,他应支付的费用为:10元;
乘坐了4千米的路程,应支付的费用为:10+(4-3)×1.3=11.3(元),
乘坐了8千米的路程,应支付的费用为:10+2×1.3+3×2.4=19.8(元),
故答案为:10;11.3,19.8;
(Ⅱ)由题意可得:10+1.3×2+2.4(x-5)=2.4x+0.6;
故答案为:2.4x+0.6或12.6+2.4(x-5)
(Ⅲ)若走5千米,则应付车费:10+1.3×2=12.6(元),
∵12.6<15,
∴此人乘车的路程超过5千米,
因此,由(Ⅱ)得2.4x+0.6=15,
解得:x=6
答:此人乘车的路程为6千米.
点评 此题主要考查了一元一次方程的应用,根据题意得出超过5km乘车费用的关系式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
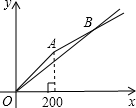 甲、乙两家商店以同样价格销售相同的商品,某次促销活动中,它们的优惠方案分别为:甲店,所有商品一律八折优惠;乙店,一次性购物中超过200元后的价格部分打六折.设商品原价为x元(x>0),购物应付金额为y元.
甲、乙两家商店以同样价格销售相同的商品,某次促销活动中,它们的优惠方案分别为:甲店,所有商品一律八折优惠;乙店,一次性购物中超过200元后的价格部分打六折.设商品原价为x元(x>0),购物应付金额为y元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
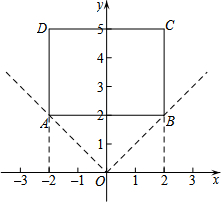 在平面直角坐标系xOy中,对图形W给出如下定义:若图形W上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形ABCD的坐标角度是90°.
在平面直角坐标系xOy中,对图形W给出如下定义:若图形W上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,如图中的矩形ABCD的坐标角度是90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
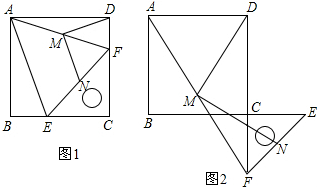
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com