
分析 (1)利用合并同类项法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变进行计算即可;
(2)根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加进行计算即可;
(3)根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加进行计算即可;
(4)根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加进行计算即可;
(5)根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加进行计算即可.
解答 解:(1)b5+b5=2b5;
(2)(-a)5•(-a)2•(-a),
=(-a)5+2+1,
=a8;
(3)-a2•a3•(-a),
=a2+3+1,
=a6;
(4)(-a)4•a3•(-a),
=a4•a3•(-a),
=-a4+3+1,
=-a8;
(5)(a-b)2•(a-b)3=(a-b)5.
点评 此题主要考查了同底数幂的乘法和合并同类项,关键是掌握同底数幂的乘法法则和合并同类项计算法则.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
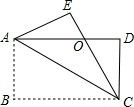 如图,把一个长方形的纸沿对角线折叠,使点B落在点E处,CE交AD于点O,若CE平分∠ACD,且AB=2$\sqrt{3}$,BC=6,则S△AOC=4$\sqrt{3}$.
如图,把一个长方形的纸沿对角线折叠,使点B落在点E处,CE交AD于点O,若CE平分∠ACD,且AB=2$\sqrt{3}$,BC=6,则S△AOC=4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
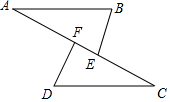 点A、F、E、C在同一条直线上,①AF=CE,②BE=DF,③BE∥DF,④∠A=∠C.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.
点A、F、E、C在同一条直线上,①AF=CE,②BE=DF,③BE∥DF,④∠A=∠C.请你从这四个条件中选出三个作为条件,另一个作为结论,组成一个真命题,并给予证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
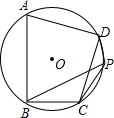 已知四边形ABCD内接于⊙O,∠D=90°,P为$\widehat{CD}$上一动点(不与点C,D重合).
已知四边形ABCD内接于⊙O,∠D=90°,P为$\widehat{CD}$上一动点(不与点C,D重合).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
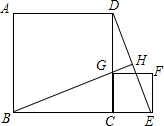 已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证:
已知,如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com