
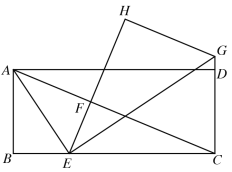
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是对角线,点
是对角线,点![]() 在线段
在线段![]() 上,连结
上,连结![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 上,点
上,点![]() 在射线
在射线![]() 上,连接
上,连接![]() ,将
,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 所在直线,则线段
所在直线,则线段![]() 的长度为( )
的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
利用勾股定理可求出AC=13,设BE=x,则EC=12-x,根据折叠的性质可得EF=BE=x,CF=13-5=8,再次利用勾股定理建立方程求出x,得到BE的长,然后求AE,最后利用△ABE∽△ECG建立比例式可求出EG.
在Rt△ABC中,
AC=![]()
设BE=x,则EC=12-x,
由折叠的性质可得∠AFE=∠B=90°,AF=AB=5,EF=BE=x,则CF=AC-AF=13-5=8
在Rt△CEF中,![]()
即![]() ,解得
,解得![]()
∴AE=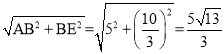 ,EC=BC-BE=
,EC=BC-BE=![]()
由折叠的性质可得∠AEB=∠AEF,∠GEH=∠GEC
∴∠AEB+∠GEC=![]()
∵∠AEB+∠BAE=90°
∴∠BAE=∠GEC,
又∵∠B=∠GCE=90°
∴△ABE∽△ECG
∴![]() ,即
,即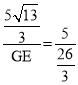
∴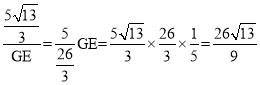
故选:B.


科目:初中数学 来源: 题型:
【题目】图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
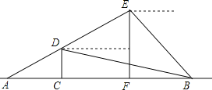
(1)分别求隧道AC和BC段的长度;
(2)建工集团安排甲、乙两个金牌施工队分别从隧道两头向中间施工,甲队负责AC段施工,乙队负责BC段施工,乙每天的工作量是甲的2倍,两队同时开工5天后,甲队将速度提高25%,乙队将速度提高了150%,从而两队同时完成,求原计划甲、乙两队每天各施工多少米.(参考数据:tan23°≈0.4,cos23°≈0.9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】佩佩宾馆重新装修后,有![]() 间房可供游客居住,经市场调查发现,每间房每天的定价为
间房可供游客居住,经市场调查发现,每间房每天的定价为![]() 元,房间会全部住满,当每间房每天的定价每增加
元,房间会全部住满,当每间房每天的定价每增加![]() 元时,就会有一间房空闲,如果游客居住房间,宾馆需对每间房每天支出
元时,就会有一间房空闲,如果游客居住房间,宾馆需对每间房每天支出![]() 元的各项费用.设每间房每天的定价增加
元的各项费用.设每间房每天的定价增加![]() 元,宾馆获利为
元,宾馆获利为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不用写出自变量的取值范围) ;
的函数关系式(不用写出自变量的取值范围) ;
(2)物价部门规定,春节期间客房定价不能高于平时定价的![]() 倍,此时每间房价为多少元时宾馆可获利
倍,此时每间房价为多少元时宾馆可获利![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
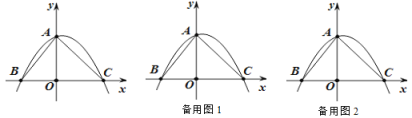
【题目】如图,抛物线y=ax2+bx+4(a≠0)与![]() 轴交于点B (-3 ,0) 和C (4 ,0)与
轴交于点B (-3 ,0) 和C (4 ,0)与![]() 轴交于点A.
轴交于点A.
(1) a = ,b = ;
(2) 点M从点A出发以每秒1个单位长度的速度沿AB向B运动,同时,点N从点B出发以每秒1个单位长度的速度沿BC向C运动,当点M到达B点时,两点停止运动.t为何值时,以B、M、N为顶点的三角形是等腰三角形?
(3) 点P是第一象限抛物线上的一点,若BP恰好平分∠ABC,请直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温润有度,为爱加温.近年来设计精巧、物美价廉的暖风机逐渐成为人们冬天必备的“取暖神器”,今年11月下旬某商场计划购进![]() 、
、![]() 两种型号的暖风机共900台,每台
两种型号的暖风机共900台,每台![]() 型号暖风机售价为600元,每台
型号暖风机售价为600元,每台![]() 型号暖风机售价为900元.
型号暖风机售价为900元.
(1)若要使得![]() 、
、![]() 两种型号暖风机的销售额不低于69万元,则至多购进多少台
两种型号暖风机的销售额不低于69万元,则至多购进多少台![]() 型号暖风机?
型号暖风机?
(2)由于质量超群、品质卓越,11月下旬购进的![]() 、
、![]() 两种型号的暖风机全部售完.该商场在12上旬又购进了
两种型号的暖风机全部售完.该商场在12上旬又购进了![]() 、
、![]() 两种型号的暖风机若干台,并且进行“双12”促销活动,每台
两种型号的暖风机若干台,并且进行“双12”促销活动,每台![]() 型号暖风机的售价比其11月下旬的售价优惠
型号暖风机的售价比其11月下旬的售价优惠![]() ,
,![]() 型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加
型号暖风机12月上旬的销售量比其在(1)问条件下的最高购进量增加![]() ,每台
,每台![]() 型号暖风机的售价比其11月下旬的售价优惠
型号暖风机的售价比其11月下旬的售价优惠![]() ,
,![]() 型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加
型号暖风机12月上旬的销售量比其在(1)问条件下的最低购进量增加![]() ,
,![]() 、
、![]() 两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了
两种型号的暖风机在12月上旬的销售额比(1)问中最低销售额增加了![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面的几何探究过程:
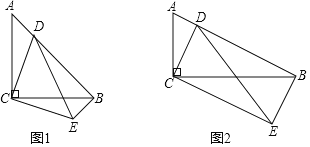
(1)观察填空
如图1,在Rt△ABC中,∠C=90°,AC=BC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°得到线段CE,连DE,BE,则
①∠CBE的度数为____________;
②当BE=____________时,四边形CDBE为正方形.
(2)探究证明
如图2,在Rt△ABC中,∠C=90°,BC=2AC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°后并延长为原来的两倍得到线段CE,连DE,BE则:
①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形
(3)拓展延伸
如图2,在点D的运动过程中,若△BCD恰好为等腰三角形,请直接写出此时AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com