
【题目】如图,四边形![]() 是菱形,
是菱形,![]() 分别是
分别是![]() 上的动点,连接
上的动点,连接![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.

【答案】![]()
【解析】
连接BQ、PB,由菱形的对角线互相垂直平分,可得B. D关于AC对称,则PB=PD,可知当B、P、Q共线时PQ+PD=PQ+BP=BQ最小,BQ为所求,当BQ⊥AD时,BQ最小,继而利用面积法求出BQ长即可得答案.
连接BQ、PB,
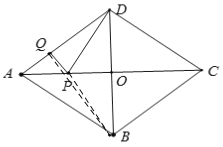
由菱形的对角线互相垂直平分,可得B. D关于AC对称,则PB=PD,
∴PQ+PD=PQ+BP,
则当B、P、Q共线时PQ+PD=PQ+BP=BQ最小,BQ为所求,当BQ⊥AD时,BQ最小,
∵四边形ABCD是菱形,AC=8,DB=6,
∴OA=4,OB=3,AC⊥BD,
在Rt△AOB中,AB=![]() =5,
=5,
∵S菱形ABCD=![]() ,
,
∴![]() ,
,
∴BQ=![]() ,
,
∴DP+PQ的最小值为![]() ,
,
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=![]() ∠BAC=60°,于是
∠BAC=60°,于是![]() =
=![]() ;
;
迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠ADE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】涡阳某童装专卖店在销售中发现,一款童装每件进价为![]() 元,销售价为
元,销售价为![]() 元时,每天可售出
元时,每天可售出![]() 件,为了迎接“六-一”儿童节,商店决定采取适当的降价措施,以扩大销售增加利润,经市场调查发现,如果每件童装降价
件,为了迎接“六-一”儿童节,商店决定采取适当的降价措施,以扩大销售增加利润,经市场调查发现,如果每件童装降价![]() 元,那么平均可多售出
元,那么平均可多售出![]() 件.
件.
(1)若每件童装降价![]() 元,每天可售出 件,每件盈利 元(用含
元,每天可售出 件,每件盈利 元(用含![]() 的代数式表示);
的代数式表示);
![]() 每件童装降价多少元时,能让利于顾客并且商家平均每天能赢利
每件童装降价多少元时,能让利于顾客并且商家平均每天能赢利![]() 元.
元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“宏扬传统文化,打造书香校园”活动中,学校计划开展四项活动:“A﹣国学诵读”、“B﹣演讲”、“C﹣课本剧”、“D﹣书法”,要求每位同学必须且只能参加其中一项活动,学校为了了解学生的意愿,随机调查了部分学生,结果统计如下:
(1)如图,希望参加活动C占20%,希望参加活动B占15%,则被调查的总人数为 人,扇形统计图中,希望参加活动D所占圆心角为 度,根据题中信息补全条形统计图.
(2)学校现有800名学生,请根据图中信息,估算全校学生希望参加活动A有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 重合).以
重合).以![]() 为边作正方形
为边作正方形![]() ,连接
,连接![]() .
.
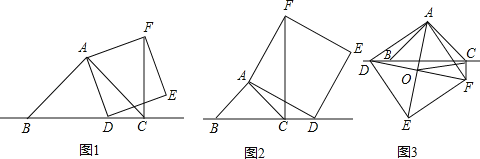
(1)如图1,当点![]() 在线段
在线段![]() 上时,求证:
上时,求证:![]() .
.
(2)如图2,当点![]() 在线段
在线段![]() 的延长线上时,其他条件不变,请直接写出
的延长线上时,其他条件不变,请直接写出![]() 三条线段之间的关系;
三条线段之间的关系;
(3)如图3,当点![]() 在线段
在线段![]() 的反向延长线上时,且点
的反向延长线上时,且点![]() 分别在直线
分别在直线![]() 的两侧.其他条件不变,若连接正方形对角线
的两侧.其他条件不变,若连接正方形对角线![]() ,交点为
,交点为![]() ,连接
,连接![]() ,探究
,探究![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
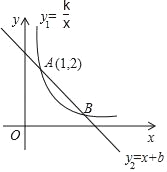
【题目】反比例函数y1=![]() (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校抽查了某班级某月10天的用电量,数据如下表:
用电量/度 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是______度,中位数是______度;
(2)求这个班级平均每天的用电量;
(3)该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com