
| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
���� ����ƽ���ı��ε��ж����������ε��ж����������ε��ж������������ε��ж����������жϼ��ɣ�
��� �⣺�ٶԽ�����ƽ�ֵ��ı�����ƽ���ı����������⣻
������ԽǷֱ���ȵ��ı�����ƽ���ı����������⣻
��һ��Ա�ƽ�У���һ��Ա���ȵ��ı�����ƽ���ı����Ǽ����⣻
��˳�����������θ����е㣬�ɵõ�һ���������������⣻
��˳�����Ӿ��θ����е㣬�ɵõ�һ�������Ǽ����⣻
�����ε������Խ��߳��ֱ�Ϊ4��6����������ε����Ϊ24�Ǽ����⣻
��ƽ���ı��ε������ڽ�ƽ������Χ�ɵ��ı����Ǿ����������⣻
�����ı��ε������Խ�����ȣ���˳�����Ӹ��ı��θ����е����õ��ı����������Ǽ����⣻
��ѡ��B��
���� ���⿼��������������жϣ���ȷ������������⣬�����������������⣮����ƽ���ı��ε��ж����������ε��ж����������ε��ж������������ε��ж������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
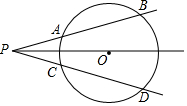 ��ͼ����P�����߷ֱ����O���ڵ�A��B��C��D������ƽ����ǡ�ù�Բ��O����֤��PA=PC��
��ͼ����P�����߷ֱ����O���ڵ�A��B��C��D������ƽ����ǡ�ù�Բ��O����֤��PA=PC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ����������Ƥ�м�ȥһ��С�����Σ�
��ͼ����һ����������Ƥ�м�ȥһ��С�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 0����1����2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com