
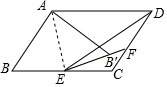
 如图,?ABCD中,E为BC上一点,将?ABCD沿AE折叠,点B落在点B′处,EB′的延长线交CD于F,EF=DF,若∠B=60°,∠BAE=40°,则∠CDE的度数为20°.
如图,?ABCD中,E为BC上一点,将?ABCD沿AE折叠,点B落在点B′处,EB′的延长线交CD于F,EF=DF,若∠B=60°,∠BAE=40°,则∠CDE的度数为20°. 分析 根据三角形内角和为180°可求∠AEB,根据折叠的性质可求∠AEB′,根据平角的定义可求∠CEF,根据平行四边形的性质可求∠C,再根据三角形内角和为180°可求∠CFE,再根据三角形外角的性质和等腰三角形的性质可求∠CDE.
解答 解:∵∠B=60°,∠BAE=40°,
∴∠AEB=180°-60°-40°=80°,
由折叠可知∠AEB′=80°,
∴∠CEF=180°-80°×2=20°,
∵四边形ABCD是平行四边形,
∴∠C=120°,
∴∠CFE=180°-120°-20°=40°,
∵EF=DF,
∴∠CDE=∠DEF,
∴∠CDE=40°÷2=20°.
故答案为:20°.
点评 考查了翻折变换(折叠问题),等腰三角形的性质,平行四边形的性质,关键是求出∠CFE的度数.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
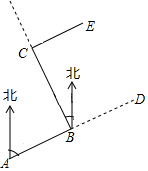 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )| A. | 80° | B. | 90° | C. | 100° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两边分别相等的两直角三角形全等 | |
| B. | 一边相等的两个正三角形全等 | |
| C. | 平行四边形是中心对称图形 | |
| D. | 菱形既是中心对称图形又是轴对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是由边长为1的小正方形组成的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形,图中已给出△ABC的一边AB的位置.
如图,是由边长为1的小正方形组成的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形,图中已给出△ABC的一边AB的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com