解:(1)对称轴为x=-
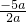
=2.5,即抛物线y=ax
2-5ax+4的对称轴是直线x=2.5;
(2)令x=0,则y=4,
∴点C的坐标为(0,4),
又∵BC∥x轴,点B,C关于对称轴对称,
∴点B的坐标为(5,4),
又∵AC=BC,
∴AC=BC=5,OA=3,点A在x轴上,
∴点A的坐标为A(-3,0),
∵抛物线y=ax
2-5ax+4经过点A,
∴9a+15a+4=0,
解得,a=-

,
∴抛物线的解析式是y=-

x
2+

x+4,
∴A,B,C三点的坐标分别是(-3,0),(5,4),(0,4),抛物线的解析式是y=-

x
2+

x+4;
(3)存在符合条件的点P共有3个.以下分三类情形探索.
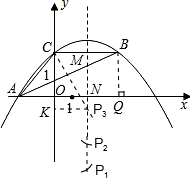
设抛物线对称轴与x轴交于N,与CB交于M.
过点B作BQ⊥x轴于Q,
易得BQ=4,AQ=8,AN=5.5,BM=

.
①以AB为腰且顶角为角A的△PAB有1个:△P
1AB.
∴AB
2=AQ
2+BQ
2=8
2+4
2=80;
在Rt△ANP
1中,P
1N
2=AP
12-AN
2=AB
2-AN
2 =80-(5.5)
2 =
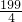
,
∴P
1(

,-
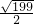
);
②以AB为腰且顶角为角B的△PAB有1个:△P
2AB.
在Rt△BMP
2中,MP
22=BP
22-BM
2=AB
2-BM
2=
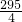
,
∴P
2(

,4-
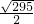
);
③以AB为底,顶角为角P的△PAB有1个,即△P
3AB.
画AB的垂直平分线交抛物线对称轴于P
3,此时平分线必过等腰△ABC的顶点C.
过点P
3作P
3K垂直y轴,垂足为K,
∵∠CP
3K=∠ABQ,∠CKP
3=∠AQB,
∴Rt△P
3CK∽Rt△BAQ.
∴P
3K:CK=BQ:AQ=1:2.
∵P
3K=2.5
∴CK=5,于是OK=1,
∴P
3(

,-1);
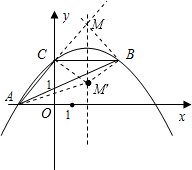
(4)直线AC交抛物线对称轴于点M,连接MB.
∵对称轴x=

是线段BC的垂直平分线,
∴MB=MC,
∴MA-MB=MA-MC=AC;
在抛物线对称轴上任取另外一点M′,则M′A-M′B=M′A-M′C<AC(三角形两边之差小于第三边),
∴线段AC为差值最大值,
根据A,C坐标得出,直线AC的解析式为y=

x+4.
则点M的坐标为(

,
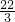
).
分析:(1)根据对称轴x=-

,代入求出即可;
(2)令x=0,求出C的坐标,根据抛物线的对称求出点B的坐标,由AB=BC=5,OA=4,得到A的坐标,代入解析式即可求出解析式;
(3)分三种情况讨论:
①以AB为腰且顶角为∠A,先求出AB的值,再利用等腰三角形的性质结合勾股定理求出P
1N的长,即可求出P
1的坐标;
②以AB为腰且顶角为角B,根据MN的长和MP
2的长,求出P
2的纵坐标,已知其横坐标,可得其坐标;
③以AB为底,顶角为角P时,依据Rt△P
3CK∽Rt△BAQ即可求出OK和P3K的长,可得P
3坐标;
(4)在抛物线的对称轴确定一点M,使|AM-BM|的值最大时,点M为直线AC与抛物线对称轴的交点.
点评:本题主要考查的是二次函数综合题.解题时,注意对线段的垂直平分线定理、勾股定理、用待定系数法求二次函数的解析式、二次函数图象上点的坐标特征等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键.

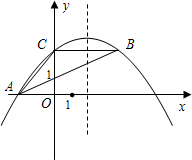 如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.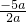 =2.5,即抛物线y=ax2-5ax+4的对称轴是直线x=2.5;
=2.5,即抛物线y=ax2-5ax+4的对称轴是直线x=2.5; ,
, x2+
x2+ x+4,
x+4, x2+
x2+ x+4;
x+4;
 .
.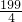 ,
, ,-
,-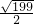 );
);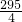 ,
, ,4-
,4-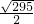 );
); ,-1);
,-1);
 是线段BC的垂直平分线,
是线段BC的垂直平分线, x+4.
x+4. ,
,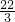 ).
). ,代入求出即可;
,代入求出即可;

 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).