
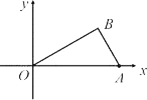
【题目】如图,已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
(1) 求点B的坐标;
(2) 若二次函数y=ax2+bx+c的图象经过A、B、O三点,求此二次函数的解析式;
(3) 在(2)中的二次函数图象的OB段(不包括点O、B)上,是否存在一点C,使得四边形ABCO的面积最大?若存在,求出这个最大值及此时点C的坐标;若不存在,请说明理由.
【答案】
【1】(![]() )
)
【2】y=![]() x2+
x2+![]() x.
x.
【3】(![]() ),
),![]()
【解析】
(1) 在Rt△OAB中,∵∠AOB=30°,∴ OB=![]() . 过点B作BD垂直于x轴,垂足为D,则 OD=
. 过点B作BD垂直于x轴,垂足为D,则 OD=![]() ,BD=
,BD=![]() ,∴点B的坐标为(
,∴点B的坐标为(![]() ) .
) .
(2) 将A(2,0)、B (![]() )、O(0,0)三点的坐标代入y=ax2+bx+c,得
)、O(0,0)三点的坐标代入y=ax2+bx+c,得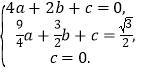
解有a=![]() ,b=
,b=![]() ,c="0." ∴所求二次函数解析式是 y=
,c="0." ∴所求二次函数解析式是 y=![]() x2+
x2+![]() x.
x.
(3) 设存在点C (x ,![]() x2+
x2+![]() x) (其中0<x<
x) (其中0<x<![]() ),使四边形ABCO面积最大.
),使四边形ABCO面积最大.
∵△OAB面积为定值,
∴只要△OBC面积最大,四边形ABCO面积就最大.
过点C作x轴的垂线CE,垂足为E,交OB于点F,则
S△OBC= S△OCF+S△BCF=![]() =
=![]() ,
,
而 |CF|=yC-yF=![]() ,
,
∴ S△OBC=![]() .
.
∴当x=![]() 时,△OBC面积最大,最大面积为
时,△OBC面积最大,最大面积为![]() .
.
此时,点C坐标为(![]() ),四边形ABCO的面积为
),四边形ABCO的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个,某学习小组进行摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再放回,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
![]() 当n很大时,估计从袋中摸出一个黑球的概率是______;
当n很大时,估计从袋中摸出一个黑球的概率是______;
![]() 试估算口袋中白球有______个;
试估算口袋中白球有______个;
![]() 在
在![]() 的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.
的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
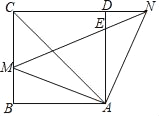
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
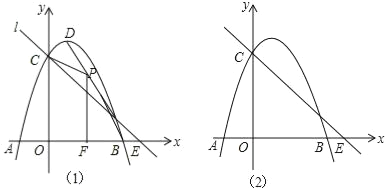
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
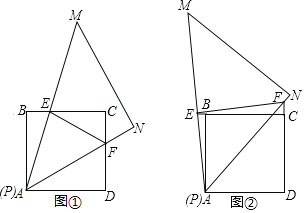
【题目】小明与同学们在数学动手实践操作活动中,将锐角为![]() 的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,
的直角三角板MPN的一个锐角顶点P与正方形ABCD的顶点A重合,正方形ABCD固定不动,然后将三角板绕着点A旋转,![]() 的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
的两边分别与正方形的边BC、DC或其延长线相交于点E、F,连结EF.
(探究发现)
![]() 在三角板旋转过程中,当
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC相交时,如图
的两边分别与正方形的边CB、DC相交时,如图![]() 所示,请直接写出线段BE、DF、EF满足的数量关系:______.
所示,请直接写出线段BE、DF、EF满足的数量关系:______.
(拓展思考)
![]() 在三角板旋转过程中,当
在三角板旋转过程中,当![]() 的两边分别与正方形的边CB、DC的延长线相交时,如图
的两边分别与正方形的边CB、DC的延长线相交时,如图![]() 所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
所示,则线段BE、DF、EF又将满足怎样的数量关系:______,并证明你的结论;
(创新应用)
![]() 若正方形的边长为4,在三角板旋转过程中,当
若正方形的边长为4,在三角板旋转过程中,当![]() 的一边恰好经过BC边的中点时,试求线段EF的长.
的一边恰好经过BC边的中点时,试求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
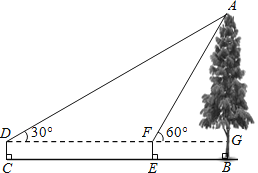
【题目】如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
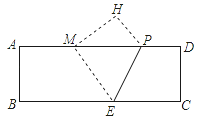
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
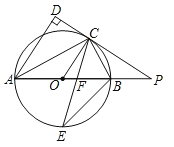
【题目】如图,已知![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上一点,
上一点,![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
(1)求证:![]() 平分
平分![]() ;
;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求圆
,求圆![]() 的半径长.
的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com