
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.

【答案】(1)详见解析;(2)AB+AC=2AE,理由详见解析.
【解析】
(1)根据相“HL”定理得出△BDE≌△CDF,故可得出DE=DF,所以AD平分∠BAC;
(2)由(1)中△BDE≌△CDE可知BE=CF,AD平分∠BAC,故可得出△AED≌△AFD,所以AE=AF,故AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.
证明:(1)∵DE⊥AB于E,DF⊥AC于F,
∴∠E=∠DFC=90°,
∴△BDE与△CDE均为直角三角形,
∵在Rt△BDE与Rt△CDF中,
![]()
∴Rt△BDE≌Rt△CDF,
∴DE=DF,
∴AD平分∠BAC;
(2)AB+AC=2AE.
理由:∵BE=CF,AD平分∠BAC,
∴∠EAD=∠CAD,
∵∠E=∠AFD=90°,
∴∠ADE=∠ADF,
在△AED与△AFD中,

∴△AED≌△AFD,
∴AE=AF,
∴AB+AC=AE﹣BE+AF+CF=AE+AE=2AE.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,横坐标为a的点 A在反比例函数
中,横坐标为a的点 A在反比例函数![]() 的图象上,点
的图象上,点![]() 与点
与点![]() 关于点
关于点![]() 对称,一次函数
对称,一次函数![]() 的图象经过点
的图象经过点![]()
(1)设![]() ,点
,点![]() (4,2)在函数
(4,2)在函数![]() ,
,![]() 的图像上.
的图像上.
①分别求函数![]() ,
,![]() 的表达式;
的表达式;
②直接写出使![]() 成立的
成立的![]() 的范围;
的范围;
(2)如图①,设函数![]() ,
,![]() 的图像相交于点
的图像相交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,△
,△![]() 的面积为16,求
的面积为16,求![]() 的值;
的值;
(3)设![]() ,如图②,过点
,如图②,过点![]() 作
作![]() 轴,与函数
轴,与函数![]() 的图像相交于点
的图像相交于点![]() ,以
,以![]() 为一边向右侧作正方形
为一边向右侧作正方形![]() ,试说明函数
,试说明函数![]() 的图像与线段
的图像与线段![]() 的交点
的交点![]() 一定在函数
一定在函数![]() 的图像上.
的图像上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经营甲、乙两种商品,其进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
已知该商店购进了甲、乙两种商品共160件.
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=![]() ,AE=4,求CD.
,AE=4,求CD.
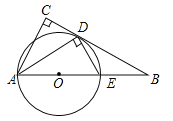
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“阳光”游泳馆为促进全民健身,2016年开始推行会员卡制度,标准如下表:
会员卡 | 办卡费用(元) | 每次游泳收费(元) |
| 50 | 25 |
| 200 | 20 |
(1)“阳光”游泳馆2016年5月销售![]() ,
,![]() 会员卡共104张,售卡收入14200元,请问这家游泳馆月销售
会员卡共104张,售卡收入14200元,请问这家游泳馆月销售![]() ,
,![]() 会员卡各多少张?
会员卡各多少张?
(2)小丽准备在“阳光”游泳馆购买会员卡,请你根据小丽游泳的次数,说明选择哪种会员卡最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AD是△ABC的中线,AE⊥AB,AF⊥AC,且AE=AB,AF=AC,AD=3,AB=4.

(1)求AC长度的取值范围;
(2)求EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com