
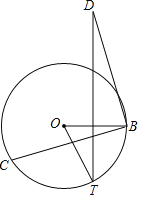
【题目】如图,C为圆O上一动点(不与点B重合),点T为圆O上一动点,且∠BOT=60°,将BC绕点B顺时针旋转90°得到BD,连接TD,当TD最大时,∠BDT的度数为_____.
【答案】7.5°
【解析】
作与圆O半径相等的圆E,圆E与圆O的直径AB相切与点B,连接TE并延长交圆E于点D,连接BD,作BC⊥BD,交圆O于点C,则BE⊥AB,在圆E上取一点F,连接TF、EF,则TE+EF>TF,由DE=EF,得出TD>TF,此时TD最大,易证△OBT是等边三角形,得出∠OBT=60°,BT=OB=BE,求出∠EBT=90°+60°=150°,∠BET=![]() (180°﹣150°)=15°,∠EDB=
(180°﹣150°)=15°,∠EDB=![]() ∠BET=7.5°,即可得出结果.
∠BET=7.5°,即可得出结果.
解:作与圆O半径相等的圆E,圆E与圆O的直径AB相切与点B,连接TE并延长交圆E于点D,连接BD,作BC⊥BD,交圆O于点C,如图所示:
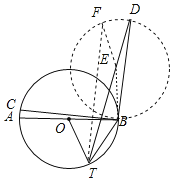
则BE⊥AB,
在圆E上取一点F,连接TF、EF,则TE+EF>TF,
∵DE=EF,
∴TD>TF,
∴此时TD最大,
∵OB=OT,∠BOT=60°,
∴△OBT是等边三角形,
∴∠OBT=60°,BT=OB=BE,
∴∠BET=∠BTE,
∵BE⊥AB,
∴∠EBT=90°+60°=150°,
∴∠BET=![]() (180°﹣150°)=15°,
(180°﹣150°)=15°,
∵ED=EB,
∴∠EDB=∠EBD,
∴∠EDB=![]() ∠BET=
∠BET=![]() ×15°=7.5°,
×15°=7.5°,
即∠BDT的度数为7.5°,
故答案为:7.5°.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
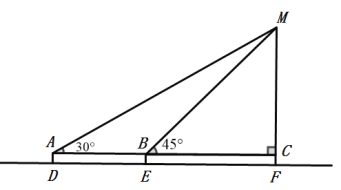
【题目】某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,请根据他们的测量数据求此楼MF的高(结果精确到0.1m,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
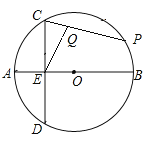
【题目】如图,![]() O的直径AB长为12,点E是半径OA的中点,过点E作CD⊥AB交
O的直径AB长为12,点E是半径OA的中点,过点E作CD⊥AB交![]() O于点C、D,点P在
O于点C、D,点P在![]() 上运动,点Q在线段CP上,且PQ=2CQ,则EQ的最大值是_________.
上运动,点Q在线段CP上,且PQ=2CQ,则EQ的最大值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
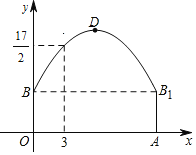
【题目】如图隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=![]() 表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为
表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.
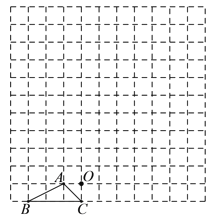
(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A1B1C1;
(2)将△A1B1C1绕点B1顺时针旋转90°,画出旋转后得到的△A2B1C2;
(3)在(2)的旋转过程中,点A1的运动路径长为 ,边A1C1扫过的区域面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,张大爷用32米长的篱笆围成一个矩形菜园,菜园一边靠墙(墙长为15米),平行于墙的一面开一扇宽度为2米的门,张大爷还在菜园内开辟出一个小区域存放化肥,两个区域用篱笆隔开,并有一扇2米的门相连(注:所有门都用其它材料).
(1)设平行于墙的一边长度为y米,垂直于墙的一边长度为x米,直接写出y与x的函数关系式,并写出自变量x的取值范围;
(2)设此时整个菜园的面积为Sm2(包括化肥存放处),则S的最大值为多少?
(3)若此时整个菜园的面积不小于81m2(包括化肥存放处),结合图象,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
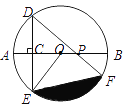
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连结EF、EO,若DE=![]() ,∠DPA=45°.
,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
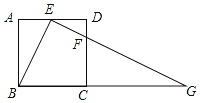
【题目】如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点,AE=ED,DF=![]() DC,连结EF并延长交BC的延长线于点G,连结BE.
DC,连结EF并延长交BC的延长线于点G,连结BE.
(1)求证:△ABE∽△DEF.
(2)若正方形的边长为4,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com