
【题目】如图,在矩形ABCD中,AC为对角线,过点B作BF⊥AC于点F,延长BF交AD于点E,交CD的延长线于点G.
(1)求证:△ABF∽△EGD;
(2)若CD=5,DG=3,求tan∠GBC的值.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)在矩形ABCD中,∠BAD=∠BCD=∠ADC=90°,AB=CD,AB∥GC,由于∠AFB=∠ADG=90°,AB∥GC,所以∠ABF=∠G,从而得证;
(2)由于∠BCD=∠AFB=90°,所以∠ACB+∠ACD=90°,∠G+∠ACD=90°,所以∠ACB=∠G,又因为∠ABC=∠BCG=90°,从而可知△ABC∽△BCG,所以BC2=CGAB,求出BC=2![]() ,所以tan∠GBC=
,所以tan∠GBC=![]()
解:(1)在矩形ABCD中,
∠BAD=∠BCD=∠ADC=90°,
AB=CD,AB∥GC,
∵BF⊥AC
∴∠AFB=∠ADG=90°,
∵AB∥GC,
∴∠ABF=∠G,
∴△ABF∽△EGD
(2)∵∠BCD=∠AFB=90°,
∴∠ACB+∠ACD=90°,∠G+∠ACD=90°,
∴∠ACB=∠G
∵∠ABC=∠BCG=90°,
∴△ABC∽△BCG,
∴![]() =
=![]() ,
,
∴BC2=CGAB,
∵CG=CD+DG=8,AB=CD=5,
∴BC=2![]()
∴tan∠GBC=![]()


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两车分别从路段AB两端同时出发,沿平行路线AC、BD行驶,CE和DF的长分别表示两车到道路AB的距离.

(1)求证:△ACE∽△BDF;
(2)如果两车行驶速度相同,求证:△ACE≌△BDF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为( )
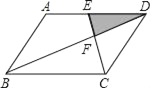
A. 8S B. 9S C. 10S D. 11S
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
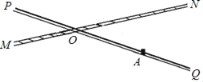
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=320m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时.
(1)居民楼是否会受到噪音的影响?请说明理由;
(2)如果行驶的速度为72km/h,居民楼受噪音影响的时间为多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一片等边三角形形状的草地,为方便人们休闲,现决定在草地内部修建一座小亭,小亭离三个出口即三角形三个顶点A、B、C的距离相等.

(1)用尺规作图的方法确定小亭的位置.
(2)若草地的边长50m,求小亭到出口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
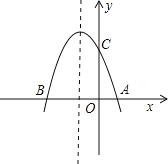
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
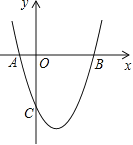
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com