练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．已知$\frac{x}{3}$=$\frac{y}{5}$，且x+y=16，则xy=60．

    分析 根据二元一次方程组的解法即可求出x与y，从而可求出xy的值．

    解答 解：∵x=$\frac{3}{5}$y，
    ∴x+y=$\frac{3}{5}$y+y=16，
    ∴y=10，
    ∴x=6，
    ∴xy=60，
    故答案为：60

    点评 本题考查二元一次方程组的解法，解题的关键是根据方程组的解法求出x与y的值，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

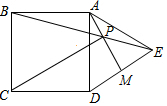    5．如图，正方形ABCD，点E为正方形外一点，△ADE为等边三角形，连BE，AM⊥DE交BE于P点，连CP．
    （1）求∠APB的度数；
    （2）求证：AP⊥CP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

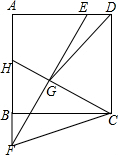    6．如图，正方形ABCD中，AB=8$\sqrt{5}$，E是AD边上一点，F是AB延长线上一点，且DE=BF，连接EF，G是EF的中点，延长CG交AB于点H，H恰好是AB的中点，连接DG，则DG的长是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

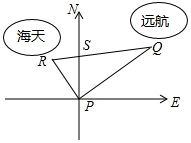    3．某港口位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定的方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口$\frac{1}{2}$小时后相距10海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．在等边△ABC中，点E在AB上，点D在CB的延长线上，且ED=EC．
    （1）如图①，若E为AB中点，求证：AE=DB．
    （2）如图②，若E为AB上任一点（端点除外），AE=DB是否仍然成立？试说明理由．
    （3）等边△ABC中，点E在直线AB上，点D在直线BC上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．一种商品按销售量分三部分制定销售单价，如表：
    销售量单价
    不超过100件的部分2.5元/件
    超过100件不超过300件的部分2.2元/件
    超过300件的部分2元/件
    （1）若买100件花250元，买300件花690元；买350件花790元；
    （2）小明买这种商品花了338元，列方程求购买这种商品多少件？
    （3）若小明花了n元（n＞250），恰好购买0.45n件这种商品，求n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．先化简再求值，（ab+1）（ab-2）+（a-2b）2+（a+2b）（-2b-a），其中a=$\frac{2}{3}$，b=-$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知|2x+3|=-2x-3，则x的取值范围是（　　）
    A．x＞-$\frac{3}{2}$B．x＜-$\frac{3}{2}$C．x≥-$\frac{3}{2}$D．x≤-$\frac{3}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．直线 y=x-1与坐标轴交于A、B两点，点C在x轴上，若△ABC为等腰三角形且S△ABC=$\frac{\sqrt{2}}{2}$，则点C的坐标为（　　）
    A．、（0，0 ）B．（1-$\sqrt{2}$，0）或（$\sqrt{2}+$1，0）C．、（$\sqrt{2}$+1，0 ）D．、（-$\sqrt{2}$-1，0）或（-$\sqrt{2}$+1，0）

    查看答案和解析>>

    同步练习册答案