
【题目】 2016湖北鄂州第23题)某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
⑴(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
⑵(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
⑶(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
【答案】(1)y=-x+50;(2)每间房价定价为320元时,每天利润最大,最大利润为9000元.(3)20.
【解析】
试题分析:(1)通过总房间50个可直接写出房间数量y与x的函数关系式;(2)设出每间房的定价,从而利用租房利润减去维护费,可得利润函数,利用配方法,即可求得结论;(3)因当日所获利润不低于5000元,由(2)知-10 (x-20) +9000≧5000;由②可知:20 (-x+50) ≦600;由③每个房间刚好住满2人可知:y个房间住满2y人,即2y=2 (-x+50),即可得出结果.
试题解析:解:⑴y=-x+50;
⑵设该宾馆房间的定价为(120+10x-20)元(x为整数),那么宾馆内有(50-x)个房间被旅客居住,依题意,得
W=(-x+50)(120+10x-20)
W=(-x+50) (10x+100)
= -10(x-20) +9000
所以当x=20,即每间房价定价为10×20+120=320元时,每天利润最大,最大利润为9000元.§科§网Z§X§⑶ 由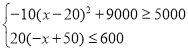
解得20 ≦ x ≦ 40)
当x=40时,这天宾馆入住的游客人数最少有: 2y=2 (-x+50)=2 (-40+50)=20 (人)


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】阅读理解并填空:
(1)为了求代数式 ![]() 的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)把一个多项式进行部分因式分解可以解决求代数式的最大(或最小)值问题.例如: ![]() =(
=( ![]() )
) ![]() =
= ![]() ,因为
,因为 ![]() 是非负数,所以,这个代数式
是非负数,所以,这个代数式 ![]() 的最小值是 , 这时相应的x的平方是.
的最小值是 , 这时相应的x的平方是.
尝试探究并解答:
(3)求代数式 ![]() 的最小值,并写出相应x的值.
的最小值,并写出相应x的值.
(4)求代数式 ![]() 的最大值,并写出相应x的值.
的最大值,并写出相应x的值.
(5)已知 ![]() ,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,A,C在一条直线上.给出下列三个事项:①AD⊥BC,EG⊥BC,垂足分别为D,G;②∠1=∠2;③AD平分∠BAC.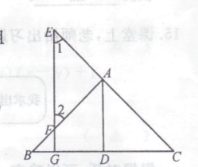
(1)以其中两个事项作为条件,另一个事项作为结论,你能组成个正确的结论;
(2)请你选择其中一个正确的结论进行说明理由.解:以为条件,为结论.(填写序号)理由是:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若x≠y,则下列各式不能成立的是( )
A.(x﹣y)2=(y﹣x)2
B.(x﹣y)3=﹣(y﹣x)3
C.(x+y)(y﹣x)=(x+y)(x﹣y)
D.(x+y)2=(﹣x﹣y)2
查看答案和解析>>
科目:初中数学 来源: 题型:
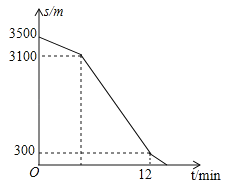
【题目】小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计)一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有4分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离s(单位:米)与他所用的时间t(单位:分钟)之间的函数关系如图所示.已知小刚从家出发7分钟时与家的距离是1200米,从上公交车到他到达学校公用10分钟.下列说法:
①公交车的速度为400米/分钟;
②小刚从家出发5分钟时乘上公交车;
③小刚下公交车后跑向学校的速度是100米/分钟;
④小刚上课迟到了1分钟.
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com