Question

(10分)如图直角坐标系中，已知A(－4，0)，B(0，3)，点M在线段A

上．

(1)如图1，如果点M是线段AB的中点，且⊙M的半径为2，试判断直线OB与⊙M的位置关系，并说明理由；

(2)如图2，⊙M与x轴、y轴都相切，切点分别是点E、F，试求出点M的坐标．

 

Answer 1

【答案】

(1)直线OB与⊙M相切．  ……………………1分

理由：

设线段OB的中点为D，连结MD．……………………2分

因为点M是线段AB的中点，所以MD∥AO，MD＝2．

所以MD⊥OB，点D在⊙M上．……………………4分

又因为点D在直线OB上，……………………5分

所以直线OB与⊙M相切．

(2) 解法一：可求得过点A、B的一次函数关系式是y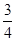＝x＋3，…………7分

因为⊙M与x轴、y轴都相切，

所以点M到x轴、y轴的距离都相等．……………………8分

设M(a，－a) (－4＜a＜0) ．

把x＝a，y＝－a代入y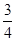＝x＋3，

得－a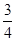＝a＋3，得a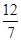＝－．……………………9分

所以点M的坐标为(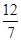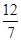－，)．……………………10分

解法二：连接ME、MF．设ME＝x(x＞0)，则OE＝MF＝x，…………6分

AE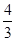＝x，所以AO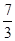＝x．………………8分

因为AO＝4，所以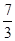，x＝4．

解得x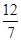＝．……………………9分

所以点M的坐标为(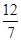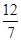－，)．……………………10分

 

【解析】略