
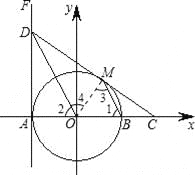
【题目】如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x 轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(﹣2,4),试求MC的长及直线DC的解析式.

【答案】见解析
【解析】试题分析:根据全等三角形、相似三角形的判断与性质以及一次函数的应用,利用全等三角形和相似三角形来得出线段相等或成比例解决本题.
(1)直线与圆的关系无非是相切,相交和相离,只要连接OM证明OM是否与DC垂直即可得出结论.
解题思路:通过证明三角形AOD和DOM全等来求解.已知的条件有OA=OM,一条公共边OD,只要证明出两组对应边的夹角相等即可.可通过OD∥MB,OM=OB来证得.
(2)求MC的长就要求出DC的长,也就是要求出AC的长.已知了D的坐标,那么AD,OA,AB的长就都知道了.
不难得出三角形OMC和DAC相似,因此可得出OM,AD,CM,AC的比例关系.已知了AD,OM的长,就能求出MC,AC的比例关系了.
在直角三角形ADC中,AD的长已知,DC=DM+MC=DA+MC,那么可根据勾股定理和MC,AC的比例关系求出MC的长.也就求出了M的坐标.有了M和D的坐标可以用待定系数法求出DC所在直线的函数解析式.
解:(1)答:直线DC与⊙O相切于点M.
证明如下:连OM,∵DO∥MB,
∴∠1=∠2,∠3=∠4.
∵OB=OM,
∴∠1=∠3.
∴∠2=∠4.
在△DAO与△DMO中, 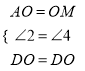 .
.
∴△DAO≌△DMO.
∴∠OMD=∠OAD.
由于FA⊥x轴于点A,
∴∠OAD=90°.
∴∠OMD=90°.即OM⊥DC.
∴DC切⊙O于M.
(2)由D(-2,4)知OA=2(即⊙O的半径),AD=4.
由(1)知DM=AD=4,由△OMC∽△DAC,知![]() .
.
∴AC=2MC,
在Rt△ACD中,CD=MC+4.
由勾股定理,有(2MC)2+42=(MC+4)2,解得MC=![]() 或MC=0(不合题意,舍去).
或MC=0(不合题意,舍去).
∴MC的长为![]() .
.
∴点C(![]() ,0).
,0).
设直线DC的解析式为y=kx+b.
则有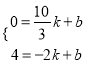 .
.
解得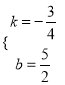 .
.
∴直线DC的解析式为y=-![]() x+
x+![]() .
.


科目:初中数学 来源: 题型:
【题目】小龙平时爱观察也喜欢动脑,他看到路边的建筑和电线架等,发现了一个现象:一切需要稳固的物品都是由三角形这个图形构成的,当时他就思考,数学王国中不仅只有三角形,为何偏偏用三角形稳固它们呢?请你用所学的数学知识解释这一现象的依据为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com