
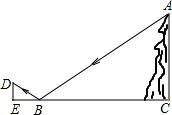
 综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为17米.
综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为17米. 科目:初中数学 来源: 题型:选择题
| A. | x≥1 | B. | x≥1且x≠±2 | C. | x≠±2 | D. | x≥1且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
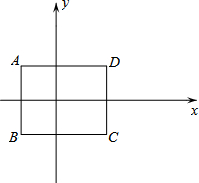 如图,在平面直角坐标系xOy中,矩形ABCD各边都平行于坐标轴,且A(-2,2),C(3,-2).对矩形ABCD及其内部的点进行如下操作:把每个点的横坐标乘以a,纵坐标乘以b,将得到的点再向右平移k(k>0)个单位,得到矩形A′B′C′D′及其内部的点(A′B′C′D′分别与ABCD对应).E(2,1)经过上述操作后的对应点记为E′.
如图,在平面直角坐标系xOy中,矩形ABCD各边都平行于坐标轴,且A(-2,2),C(3,-2).对矩形ABCD及其内部的点进行如下操作:把每个点的横坐标乘以a,纵坐标乘以b,将得到的点再向右平移k(k>0)个单位,得到矩形A′B′C′D′及其内部的点(A′B′C′D′分别与ABCD对应).E(2,1)经过上述操作后的对应点记为E′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
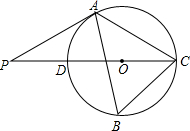 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
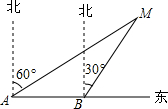 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )| A. | 10分钟 | B. | 15分钟 | C. | 20分钟 | D. | 25分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com