
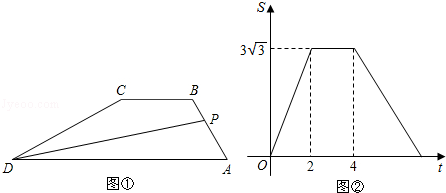
 �ף����������630ǧ�ף��ͳ��Ӽس������ҵ�������ʻ��ͬʱ�������ҵس��������������ʻ���ڼ������ؼ���һ��;վP���������ٶ��ǿͳ���$\frac{3}{4}$���͡�������Pվ�ľ���ֱ�Ϊy1��y2��ǧ�ף�����������ʻʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��ٿͳ����ٶ�Ϊ60ǧ��/Сʱ���ڻ������ٶ�Ϊ45ǧ��/Сʱ��������������ʱ��Ϊ6Сʱ���ܵ�E������Ϊ��14��540����˵����ȷ�ĸ����У�����������
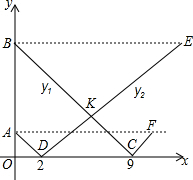
�ף����������630ǧ�ף��ͳ��Ӽس������ҵ�������ʻ��ͬʱ�������ҵس��������������ʻ���ڼ������ؼ���һ��;վP���������ٶ��ǿͳ���$\frac{3}{4}$���͡�������Pվ�ľ���ֱ�Ϊy1��y2��ǧ�ף�����������ʻʱ��x��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ��ٿͳ����ٶ�Ϊ60ǧ��/Сʱ���ڻ������ٶ�Ϊ45ǧ��/Сʱ��������������ʱ��Ϊ6Сʱ���ܵ�E������Ϊ��14��540����˵����ȷ�ĸ����У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �٢���ͳ����ٶ�Ϊa km/h����������ٶ�Ϊ$\frac{3}{4}$km/h�����������г�һԪһ�η�����⼴�ɣ�
�۸��������г�����������ϵʽ����y1=y2ʱ���ⷽ�̼��ɣ�
������������������꣮
��� �⣺��ͳ����ٶ�Ϊa km/h����������ٶ�Ϊ$\frac{3}{4}$km/h���������з��̵ã�
9a+$\frac{3}{4}$��2=630��
���a=60��
��$\frac{3}{4}$a=45��
�𣺿ͳ����ٶ�Ϊ60 km/h���������ٶ�Ϊ45km/h��
�ʢ٢���ȷ��
��P��14��540����D ��2��0����
��y2=45x-90��
��F��9��0��M��0��540����
��y1=-60x+540��
��$\left\{\begin{array}{l}{y=-60x+540}\\{y=45x-90}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=6}\\{y=180}\end{array}\right.$��
��E ��6��180����
����ʻ6Сʱʱ������������
�ʢ���ȷ���ܴ���
��ȷ��ѡ����3����
��ѡ��C��
���� ���⿼����һ�κ�����Ӧ�ü�һԪһ�η��̵�Ӧ�ã�����Ĺؼ��Ǹ���������ͼ��˵����ͼ���ʾ��ʵ�����壬���������������⼰��ȷ�Ľ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ�����ƽ�ֵ��ı�����ƽ���ı��� | |
| B�� | ��������������� | |
| C�� | ����1��3��6��1��2��2��������2 | |
| D�� | ���麽��ɻ����㲿���Ƿ�ϸ�����ȫ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8�� | B�� | ��4+$2\sqrt{3}$���� | C�� | ��4+3$\sqrt{3}$���� | D�� | ��4+$\sqrt{3}$���� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com