
分析 先化简题目中的式子,然后将a+b=-10,ab=8代入化简后的式子即可解答本题.
解答 解:∵a+b=-10,ab=8,
∴a<0,b<0,
∴a$\sqrt{\frac{a}{b}}$+b$\sqrt{\frac{b}{a}}$
=$-\frac{a\sqrt{ab}}{b}-\frac{b\sqrt{ab}}{a}$
=$-\frac{{a}^{2}\sqrt{ab}+{b}^{2}\sqrt{ab}}{ab}$
=$-\frac{\sqrt{ab}[(a+b)^{2}-2ab]}{ab}$
=$-\frac{\sqrt{8}[(-10)^{2}-2×8]}{8}$
=$-\frac{2\sqrt{2}×84}{8}$
=-21$\sqrt{2}$.
∴a$\sqrt{\frac{a}{b}}$+b$\sqrt{\frac{b}{a}}$
=$\frac{a\sqrt{ab}}{b}+\frac{b\sqrt{ab}}{a}$
=$\frac{{a}^{2}\sqrt{ab}+{b}^{2}\sqrt{ab}}{ab}$
=$\frac{({a}^{2}+{b}^{2})\sqrt{ab}}{ab}$
=$\frac{[(a+b)^{2}-2ab]\sqrt{ab}}{ab}$
=$\frac{[(-10)^{2}-2×8]×\sqrt{8}}{8}$
=$\frac{(100-16)×2\sqrt{2}}{8}$
=$\frac{84×2\sqrt{2}}{8}$
=21$\sqrt{2}$.
点评 本题考查二次根式的化简求值,解题的关键是明确二次根式化简求值的方法.


科目:初中数学 来源: 题型:解答题
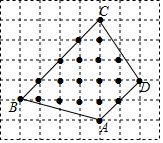 我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长度.S为图形的面积,L是边界上的格点数,N是内部格点数,则有S=$\frac{L}{2}$+N-1.请根据此方法计算图中四边形ABCD的面积.
我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长度.S为图形的面积,L是边界上的格点数,N是内部格点数,则有S=$\frac{L}{2}$+N-1.请根据此方法计算图中四边形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图:在△ABC中,BE、CD分别是AC、AB边上的中线,BE与CD相交于点O,则$\frac{BO}{BE}$=( )
如图:在△ABC中,BE、CD分别是AC、AB边上的中线,BE与CD相交于点O,则$\frac{BO}{BE}$=( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com