
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井.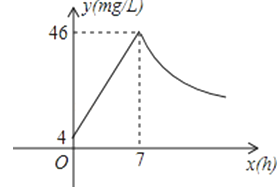
【答案】解:(1)因为爆炸前浓度呈直线型增加,
所以可设y与x的函数关系式为y=k1x+b(k1≠0),
由图象知y=k1x+b过点(0,4)与(7,46),
则![]() ,
,
解得![]() ,
,
则y=6x+4,此时自变量x的取值范围是0≤x≤7.
(不取x=0不扣分,x=7可放在第二段函数中)
∵爆炸后浓度成反比例下降,
∴可设y与x的函数关系式为y=![]() (k2≠0).
(k2≠0).
由图象知y=![]() 过点(7,46),
过点(7,46),
∴![]() =46,
=46,
∴k2=322,
∴y=![]() ,此时自变量x的取值范围是x>7.
,此时自变量x的取值范围是x>7.
(2)当y=34时,由y=6x+4得,6x+4=34,x=5.
∴撤离的最长时间为7﹣5=2(小时).
∴撤离的最小速度为3÷2=1.5(km/h).
(3)当y=4时,由y=![]() 得,x=80.5,
得,x=80.5,
80.5﹣7=73.5(小时).
∴矿工至少在爆炸后73.5小时才能下井.
【解析】(1)根据图象可以得到函数关系式,y=k1x+b(k1≠0),再由图象所经过点的坐标(0,4),(7,46)求出k1与b的值,然后得出函数式y=6x+4,从而求出自变量x的取值范围.再由图象知y=![]() (k2≠0)过点(7,46),求出k2的值,再由函数式求出自变量x的取值范围.
(k2≠0)过点(7,46),求出k2的值,再由函数式求出自变量x的取值范围.
(2)结合以上关系式,当y=34时,由y=6x+4得x=5,从而求出撤离的最长时间,再由v=![]() 速度.
速度.
(3)由关系式y=![]() 知,y=4时,x=80.5,矿工至少在爆炸后80.5﹣7=73.5(小时)才能下井.
知,y=4时,x=80.5,矿工至少在爆炸后80.5﹣7=73.5(小时)才能下井.


科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.
(1)求乙、丙两台机器每小时各生产多少个?
(2)由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.
①若生产次序为甲、乙、丙,则最后一个芭比娃娃由 机器生产完成,整个生产过程共需 小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
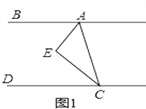
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
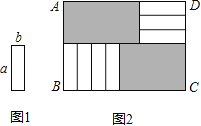
A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 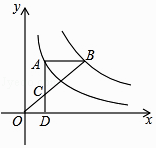
A.6
B.9
C.10
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(m,n)在y=![]() 的图象上,且m(n﹣1)≥0.
的图象上,且m(n﹣1)≥0.
(1)求m的取值范围;
(2)当m,n为正整数时,写出所有满足题意的A点坐标,并从中随机抽取一个点,求:在直线y=﹣x+6下方的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上的一点(点
上的一点(点![]() 不与点
不与点![]() ,
,![]() 重合).过点
重合).过点![]() ,点
,点![]() 作直线
作直线![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 和点
和点![]() .
.
图1. 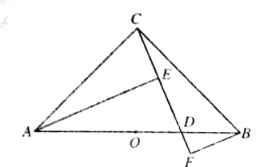 图2.
图2. 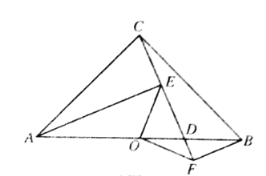
(1)如图1,求证:![]() ;(2)如图2,连接
;(2)如图2,连接![]() ,
,![]() ,请判断线段
,请判断线段![]() 与
与![]() 之间的数量关系和位置关系,并说明理由.
之间的数量关系和位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com