
【题目】定义:![]() 是关于
是关于 ![]() ,
,![]() 的多项式,如果
的多项式,如果 ![]() ,那么
,那么 ![]() 叫做“对称多项式”.例如,如果
叫做“对称多项式”.例如,如果 ![]() ,则
,则 ![]() 显然 ,所以
显然 ,所以 ![]() 是“对称多项式”.
是“对称多项式”.
(1)![]() 是“对称多项式”,试说明理由;
是“对称多项式”,试说明理由;
(2)请写一个“对称多项式”,![]() (不多于四项);
(不多于四项);
(3)如果 ![]() 和
和 ![]() 均为“对称多项式”,那么
均为“对称多项式”,那么 ![]() 一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
一定是“对称多项式”吗?如果一定,请说明理由,如果不一定,请举例说明.
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°.

(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①![]() ,②
,②![]() ,③
,③![]() 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.

(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:

(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,回答问题
距离能够产生美.
唐代著名文学家韩愈曾赋诗:“天街小雨润如酥,草色遥看近却无.
当代印度著名诗人泰戈尔在《世界上最遥远的距离》中写道:
“世界上最遥远的距离
不是瞬间便无处寻觅
而是尚未相遇
便注定无法相聚”
距离是数学、天文学、物理学中的热门话题,唯有对宇宙距离进行测量,人类才能掌握世界尺度.
已知点 A,B 在数轴上分别表示有理数 a,b,A,B 两点之间的距离表示为 AB.
(![]() )当 A,B 两点中有一点在原点时,不妨设点 A 在原点,如图 1,
)当 A,B 两点中有一点在原点时,不妨设点 A 在原点,如图 1,![]() .
.
(![]() )当 A,B 两点都不在原点时,
)当 A,B 两点都不在原点时,
①如图 2,点 A,B 都在原点的右边,![]() ;
;
②如图 3,点 A,B 都在原点的左边,![]() ;
;
③如图 4,点 A,B 在原点的两边,![]() .
.
综上,数轴上 A,B 两点的距离 ![]() .
.
利用上述结论,回答以下三个问题:
![]()
(1)若数轴上表示 ![]() 和
和![]() 的两点之间的距离是
的两点之间的距离是![]() ,则
,则 ![]() ;
;
(2)若代数式 ![]() 取最小值时,则
取最小值时,则![]() 的取值范围是 ;
的取值范围是 ;
(3)若未知数 ![]() ,
,![]() 满足
满足 ![]() ,则代数式
,则代数式 ![]() 的最大值是 ,最小值是 .
的最大值是 ,最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x=﹣4与x轴交于点E,一开口向上的抛物线过原点交线段OE于点A,交直线x=﹣4于点B,过B且平行于x轴的直线与抛物线交于点C,直线OC交直线AB于D,且AD:BD=1:3.
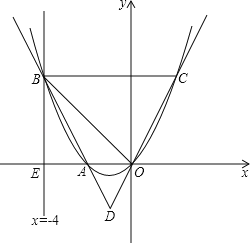
(1)求点A的坐标;
(2)若△OBC是等腰三角形,求此抛物线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
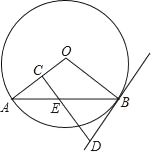
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一批学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟的态度(分三类:A表示主动制止;B表示反感但不制止,C表示无所谓)进行了问卷调查,根据调查结果分别绘制了如下两个统计图. 请根据图中提供的信息解答下列问题:
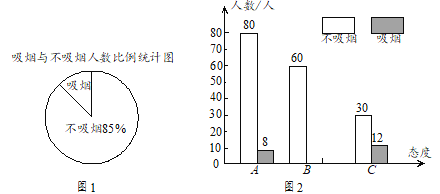
(1)图1中,“吸烟”类人数所占扇形的圆心角的度数是多少?
(2)这次被调查的市民有多少人?
(3)补全条形统计图;
(4)若该市共有市民480万人,求该市大约有多少人吸烟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com