
【题目】已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b﹣1)2=0,A、B之间的距离记作|AB|,定义:|AB|=|a﹣b|.
(1)求线段AB的长|AB|;
(2)设点P在数轴上对应的数为x,当|PA|﹣|PB|=2时,求x的值;
(3)若点P在A的左侧,M、N分别是PA、PB的中点,当P在A的左侧移动时,下列两个结论:
①|PM|+|PN|的值不变;②|PN|﹣|PM|的值不变,其中只有一个结论正确,请判断出正确结论,并求其值.
【答案】(1)5;(2)![]() ;(3) ②;
;(3) ②; ![]() .
.
【解析】
试题(1)应用非负数的性质得,a+4=0,b-1=0,解得a和b的值,进而求得|AB|的值;
(2)应考虑到A、B、P三点之间的位置关系的多种可能解题;
(3)当P在A的左侧移动时,设点P对应的数为x,列式求出|PN|-|PM|的值即可.
试题解析:解:(1)由题意得a+4=0,b-1=0,解得a=-4,b=1,所以|AB|=1-(-4)=5;
(2)当P在点A左侧时,|PA|-|PB|=-(|PB|-|PA|)=-|AB|=-5≠2,
当P在点B右侧时,|PA|-|PB|=|AB|=5≠2,
∴上述两种情况的点P不存在,
当P在A、B之间时,|PA|=|x-(-4)|=x+4,|PB|=|x-1|=1-x,
∵|PA|-|PB|=2,∴(x+4)-(1-x)=2,∴x=![]() ;
;
![]() ,
,![]() ,
,![]()
(3)第②个结论正确,|PN|-|PM|=![]() .
.
∵|PN|-|PM|=![]() (|PB|-|PA|)=
(|PB|-|PA|)=![]() |AB|=
|AB|=![]() .
.


科目:初中数学 来源: 题型:
【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.

(1).请用两种不同的方法表示图中阴影部分的面积.
方法①: ;
方法②: .
(2).由 (1)可得出![]() 2,
2,![]() ,4mn这三个代数式之间的一个等量关系为: .
,4mn这三个代数式之间的一个等量关系为: .
(3)利用(2)中得到的公式解决问题:已知2a+b=6,ab=4,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的角平分线AD交BC于E,交△ABC的外接圆⊙O于D. 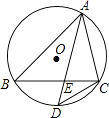
(1)求证:△ABE∽△ADC;
(2)请连接BD,OB,OC,OD,且OD交BC于点F,若点F恰好是OD的中点.求证:四边形OBDC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂仓库储存了部分原料,按原计划每时消耗2 t,可用60 h.由于技术革新,实际生产能力有所提高,即每时消耗的原料量大于计划消耗的原料量.设现在每时消耗原料x(单位:t),库存的原料可使用的时间为y(单位:h).
(1)写出y关于x的函数解析式,并求出自变量的取值范围;
(2)若恰好经过24 h才有新的原料进厂,为了使机器不停止运转,则x应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是(把你认为正确结论的序号都填上.) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输队要运300 t物资到江边防洪.
(1)运输时间t(单位:h)与运输速度v(单位:t/h)之间有怎样的函数关系式?
(2)运了一半时,接到防洪指挥部命令,剩下的物资要在2 h之内运到江边,则运输速度至少为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com