
科目:初中数学 来源: 题型:
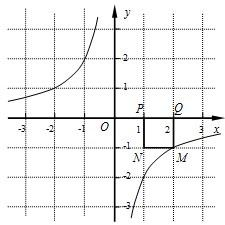 已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-| 2 |
| x |
| 2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
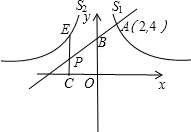 如图,已知点A(2,4)在反比例函数y=
如图,已知点A(2,4)在反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 (2012•贵阳模拟)阅读下列材料:
(2012•贵阳模拟)阅读下列材料:| 2 | x |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市绿城育华学校九年级(上)月考数学试卷(9月份)(解析版) 题型:解答题
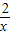 的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.
的图象上.小明对上述问题进行了探究,发现不论m取何值,符合上述条件的正方形只有两个,且一个正方形的顶点M在第四象限,另一个正方形的顶点M1在第二象限.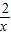 ,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.
,P点坐标为(1,0),图中已画出一符合条件的一个正方形PQMN,请你在图中画出符合条件的另一个正方形PQ1M1N1,并写出点M1的坐标;M1的坐标是______.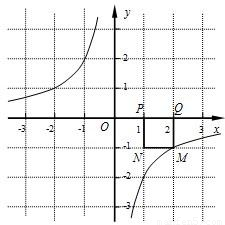
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com