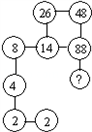
分析:(1)观察发现,从第4个数开始,每一个数都是它的前三个数的和,依此规律求解即可.
(2)分别找到分子和分母的指数的变化规律即可找到分式的变化规律,另外还需得到他们符号的规律.
解答:解:(1)∵8=4+2+2,
14=8+4+2,
26=14+8+4,
48=26+14+8,
88=48+26+14,
∴?=88+48+26=162.
(2)∵这一列数的分母a的指数分别是1、2、3、4…,与这列数的项数相同,
∴第7个式子的分母是a
7,第n个式子的分母是a
n;
∵这一列数的分子b的指数分别是2、5、8、11,…,
即:第一个数是3×1-1=2,
第二个数是3×2-1=5,
第三个数是3×3-1=8,
第四个数是3×4-1=11,…,
∴每个数都比项数的3倍少1,
∴第7个式子的分子是b
3×7-1=b
20,第n个式子的分子是b
3n-1;
∵它们符号的规律是奇数项为负,偶数项为正,
∴第7个式子的符号为负,第n个式子的符号为(-1)
n.
∴第7个式子是-
,第n个式子是(-1)
n.
故答案为:(1)162;(2)-
,(-1)
n.
点评:本题是对数字变化规律题目的考查,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.对于本题第(2)题而言难点就是变化的部分太多,有三处发生变化:分子、分母、分式的符号.同学们很容易发现各部分的变化规律,但是如何用一个统一的式子表示出分式的符号的变化规律是难点中的难点.

 (1)观察如图寻找规律,在“?”处填上的数字是
(1)观察如图寻找规律,在“?”处填上的数字是

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案


 (1)观察如图寻找规律,在“?”处填上的数字是________;
(1)观察如图寻找规律,在“?”处填上的数字是________; ,…(ab≠0),其中第7个式子是________,第n个式子是________(n为正整数)
,…(ab≠0),其中第7个式子是________,第n个式子是________(n为正整数)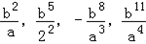 ,…(ab≠0),其中第7个式子是_________,第n个式子是_________(n为正整数)
,…(ab≠0),其中第7个式子是_________,第n个式子是_________(n为正整数)