
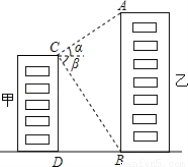
(10分)如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30°,测得乙楼底部B点的俯角β为60°,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
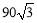 ;
; .
.
【解析】
试题分析:作CE⊥AB于点E,在Rt△ACE和Rt△BCE中,利用tanβ=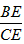 ,和tanα=
,和tanα= ,可求出BE、AE的长,然后可解决问题.
,可求出BE、AE的长,然后可解决问题.
试题解析:作CE⊥AB于点E,

∵CE∥DB,CD∥AB,且∠CDB=90°,
∴四边形BECD是矩形,
∴CD=BE,CE=BD,
在Rt△BCE中,β=60°,CE=BD=90米,
∵tanβ=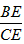 ,
,
∴BE=CE·tanβ=90×tan60°=90 (米),
(米),
∴CD=BE=90 (米),
(米),
在Rt△ACE中,α=30°,CE=90米,
∵tanα= ,
,
∴AE=CE·tanα=90×tan30°=90×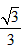 =30
=30 (米),
(米),
∴AB=AE+BE=30 +90
+90 =120
=120 (米),
(米),
答:甲楼高为90 米,乙楼高为120
米,乙楼高为120 米.
米.
考点:解直角三角形的应用.


科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:选择题
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
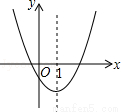
A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)沿海开发公司准备投资开发A、B两种新产品,通过市场调研发现:
(1)若单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;
(2)若单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
(3)根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值如下表所示:

(1)填空:yA= ;yB= ;
(2)若公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),试写出W与某种产品的投资金额x(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:填空题
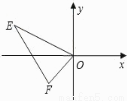
已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点E′的坐标为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
某种药品原价为36元/盒.经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A.36(1-x)2=36-25 B.36 (1-2x) =25
C.36(1-x)2=25 D.36(1-x2)=25
查看答案和解析>>
科目:初中数学 来源: 题型:
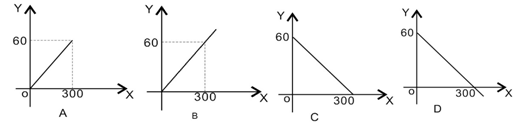
一辆汽车的油箱中现有汽油60升,如果不再加油,那么油箱中的油量y(升)随行驶里程x(千米)的增加而减少,若这辆汽车平均耗油量为0.2升/千米,则y与x之间的函数关系用图象表示,大致是 ( )、
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )
A (-3,0) B (-1,6) C (-3,-6) D (-1,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com