
分析 先分别求出-2-$\sqrt{5}$和3-$\sqrt{2}$的范围,再求出整数解即可.
解答 解:∵2<$\sqrt{5}$<3,
∴-2>-$\sqrt{5}$>-3,
∴-4>-2-$\sqrt{5}$>-5,
∵1<$\sqrt{2}$<2,
∴-1>-$\sqrt{2}$>-2,
∴2>3-$\sqrt{2}$>1,
∴大于-2-$\sqrt{5}$,且不大于3-$\sqrt{2}$的非正整数有-4,-3,-2,-1,0,1,
故答案为:-4,-3,-2,-1,0,1.
点评 本题考查了估算无理数的大小,实数的大小比较的应用,能求出-2-$\sqrt{5}$和3-$\sqrt{2}$的范围是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,A、B两地相距50千米.甲于某日下午1时骑自行车从A地驶往B地,乙也于同日下午骑摩托车按同路从A地出发出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米.甲于某日下午1时骑自行车从A地驶往B地,乙也于同日下午骑摩托车按同路从A地出发出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:填空题
下列二次根式,不能与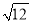 合并的是______(填写序号即可).
合并的是______(填写序号即可).
①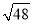 ; ②
; ② ; ③
; ③ ; ④
; ④ ; ⑤
; ⑤ .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com