
【题目】二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为-8、2,求二次函数的解析式
【答案】![]() 或
或![]()
【解析】
根据一元二次方程ax2+bx+c=0的两根为-8、2可得抛物线与x轴交点坐标为(-8,0)、(2,0),然后分开口向上与开口向下两种情况分类讨论进一步求解即可,
∵二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,且一元二次方程ax2+bx+c=0的两根为-8、2,
∴当x=-8时,y=0;x=2时,y=0,
∵tan∠ABC=3,
∴OC=6,
当抛物线开口向上时,C点坐标为(0,-6),
∴![]() ……①
……①
![]() ……②
……②
结合①②可得:![]() ,
,![]() ,
,
∴二次函数解析式为:![]() ;
;
当抛物线开口向下时,C点坐标为(0,6),
∴![]() ……③
……③
![]() ……④
……④
结合③④可得:![]() ,
,![]() ,
,
∴二次函数解析式为:![]() ,
,
综上所述,抛物线解析式为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是第一象限内横坐标为2的一个定点,
是第一象限内横坐标为2的一个定点,![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,若点
,若点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 点不变,
点不变,![]() 点随之运动,当点
点随之运动,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 运动的路径长是( )
运动的路径长是( )

A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
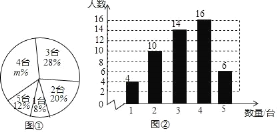
【题目】随着移动计算技术和无线网络的快速发展,移动学习方式越来越引起人们的关注,某校计划将这种学习方式应用到教育学中,从全校1500名学生中随机抽取了部分学生,对其家庭中拥有的移动设备的情况进行调查,并绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中m的值为 ;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校1500名学生家庭中拥有3台移动设备的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
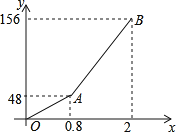
【题目】元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出AB段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,在平面直角坐标系中,二次函数![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.

(1)求二次函数的表达式;
(2)点![]() 是第二象限内的点抛物线上一动点
是第二象限内的点抛物线上一动点
①求![]() 面积最大值并写出此时点
面积最大值并写出此时点![]() 的坐标;
的坐标;
②若![]() ,求此时点
,求此时点![]() 坐标;
坐标;
(3)连接![]() ,点
,点![]() 是线段
是线段![]() 上的动点.连接
上的动点.连接![]() ,把线段
,把线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 是点
是点![]() 的对应点.当动点
的对应点.当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,则动点
,则动点![]() 所经过的路径长等于______(直接写出答案)
所经过的路径长等于______(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论:①b2﹣4ac=0 ②a+b+c>0 ③2a﹣b=0④c﹣a=3,其中正确的有_____.(填序号)
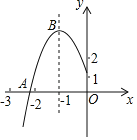
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限内的点C分别在双曲线![]() 和
和![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
①阴影部分的面积为![]() ;
;
②若B点坐标为(0,6),A点坐标为(2,2),则![]() ;
;
③当∠AOC=![]() 时,
时,![]() ;
;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是 ____________(填写正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球,放回、搅匀,下表是活动进行中的一组统计数据,
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.230 | 0.231 | 0.300 | 0.260 | 0.254 |
袋中白球的个数约为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
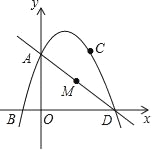
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com