
【题目】如图,二次函数y=ax2+bx+c的图象过点A(3,0),对称轴为直线x=1,给出以下结论:①abc<0;②b2﹣4ac>0;③a+b+c≥ax2+bx+c;④若M(x2+1,y1)、N(x2+2,y2)为函数图象上的两点,则y1<y2,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】A
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
∵抛物线开口向下,
a<0;
∵抛物线的对称轴为直线x=-![]() =1>0,
=1>0,
∴b>0;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,故①正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,故②正确;
∵抛物线的对称轴是x=1,与x轴的一个交点是(3,0),
∴抛物线与x轴的另个交点是(-1,0),
∴当x=1时,y最大,即a+b+c≥ax2+bx+c,故③正确;
∵B(x2+1,y1)、C(x2+2,y2)在对称轴右侧,x2+1<x2+2,
∴y1>y2,故④错误;
故选A.


科目:初中数学 来源: 题型:
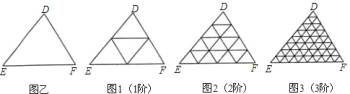
【题目】一般地,“任意三角形都是自相似图形”,只要顺次连接三角形各边中点,则可将原三角形分割为四个都与它自己相似的小三角形.我们把![]() (图乙)第一次顺次连接各边中点所进行的分割,称为
(图乙)第一次顺次连接各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() );把
);把![]() 阶分割得出的
阶分割得出的![]() 个三角形再分别顺次连接它的各边中点所进行的分割,称为
个三角形再分别顺次连接它的各边中点所进行的分割,称为![]() 阶分割(如图
阶分割(如图![]() )…,依此规则操作下去.
)…,依此规则操作下去.![]() 阶分割后得到的每一个小三角形都是全等三角形(
阶分割后得到的每一个小三角形都是全等三角形(![]() 为正整数),设此时小三角形的面积为
为正整数),设此时小三角形的面积为![]() .请写出一个反映
.请写出一个反映![]() ,
,![]() ,
,![]() 之间关系的等式________.
之间关系的等式________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.
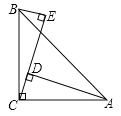
(1)直线BE与AD的位置关系是 ;BE与AD之间的距离是线段 的长;
(2) 若AD=6cm,BE=2cm.,求BE与AD之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,△ABC的三个顶点在互相平行的三条直线l1,l2,l3上,且l1,l2之间的距离是1,l2,l3之间的距离是2,则BC的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本事实:两角及其夹边分别相等的两个三角形全等(简称![]() ).请你在此基础上解决下面问题:
).请你在此基础上解决下面问题:

(1)叙述三角形全等的判定方法中的![]() ;
;
(2)证明![]() .要求:叙述要用文字表达;用图形中的符号表达已知、求证,并证明,证明时各步骤要注明依据.
.要求:叙述要用文字表达;用图形中的符号表达已知、求证,并证明,证明时各步骤要注明依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化成一元二次方程的一般形式.
的方程,并将其化成一元二次方程的一般形式.
(1)4个完全相同的正方形的面积之和是25,求正方形的边长![]() .
.
(2)一个矩形的长比宽多2,面积是100,求矩形的长![]() .
.
(3)一个直角三角形的斜边长为10,两条直角边相差2,求较长的直角边长![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com