
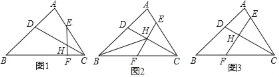
【题目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分别是AC,BC边上的两点,EF交于CD于H,
(1)如图1,若∠EFC=∠A,求证:CECD=CHBC;
(2)如图2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的长;
(3)如图3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)2![]() ; (3)
; (3)![]() .
.
【解析】
(1)只要证明△ECH∽△BCD,可得![]() =
=![]() ,即可推出CECD=CHBC;
,即可推出CECD=CHBC;
(2)如图2中,连接AH.只要证明△AEH∽△HFB,可得![]() =
=![]() ,推出FH2=6,推出HE=HF=
,推出FH2=6,推出HE=HF=![]() ,即可解决问题.
,即可解决问题.
(3)只要证明△ECF∽△BCA,求出CF即可解决问题.
(1)证明:如图1中,
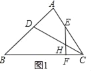
∵∠EFC+∠FEC+∠ECF=180°,∠A+∠B+∠ACB=180°,
又∵∠EFC=∠A,∠ECF=∠ACB,
∴∠CEF=∠B,∵∠ECH=∠DCB,
∴△ECH∽△BCD,
∴![]() ,
,
∴CECD=CHBC.
(2)解:如图2中,连接AH.
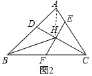
∵BH、CH都是△ABC的角平分线,
∴AH是△ABC的角平分线,
∴∠BHC=180°﹣![]() (∠ABC+∠ACB)=180°﹣
(∠ABC+∠ACB)=180°﹣![]() (180°﹣∠BAC)=90°+
(180°﹣∠BAC)=90°+![]() BAC=90°+∠HAE,
BAC=90°+∠HAE,
∵CE=CF,∠HCE=∠HCF,
∴CH⊥EF,HF=HE,
∴∠CHF=90°,
∵∠BHC=∠BHF+∠CHF=∠BHF+90°,
∴∠HAE=∠BHF,
∵∠CFE=∠CEF,
∴∠AEH=∠BFH,
∴△AEH∽△HFB,
∴![]() ,
,
∴FH2=6,
∴HE=HF=![]() ,
,
∴EF=2![]() .
.
(3)解:如图3中,作HM⊥AC于M,HN⊥BC于N.设HF=x,FN=y.
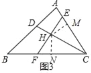
∵∠HCM=∠HCN=30°,HC=5,
∴HM=HN=![]() span>,CM=CN=
span>,CM=CN=![]() ,
,
∵CE=4![]() ,
,
∴EM=![]() ,EH=
,EH=![]() ,
,
∵S△HCF:S△HCE=FH:EH=FC:EC,
∴x:![]() =(y+
=(y+![]() ):4
):4![]() ①,
①,
又∵x2=y2+(![]() )2,
)2,
解得y=![]() 或
或![]() (舍弃),
(舍弃),
∴CF=![]() ,
,
∵∠CEF=∠B,∠ECF=∠ACB,
∴△ECF∽△BCA,
∴![]() ,
,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,△ABC各顶点的坐标分别为:A(4,0),B(﹣1,4),C(﹣3,1)
(1)在图中作△A′B′C′使△A′B′C′和△ABC关于x轴对称;
(2)写出点A′B′C′的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE,CD分别为其角平分线且交于点O.
(1)当∠A=60°时,求∠BOC的度数;
(2)当∠A=100°时,求∠BOC的度数;
(3)当∠A=α时,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是( )

(A)AB=BE (B)BE⊥DC (C)∠ADB=90° (D)CE⊥DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
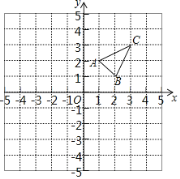
(1)作出与△ABC关于x轴对称的△A1B1C1;
(2)将△ABC向左平移4个单位长度,画出平移后的△A2B2C2;
(3)若在如图的网格中存在格点P,使点P的横、纵坐标之和等于点C的横、纵坐标之和,请写出所有满足条件的格点P的坐标(C除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一抛物线的顶点![]() 的坐标是
的坐标是![]() ,并且抛物线与
,并且抛物线与![]() 轴两交点间的距离为
轴两交点间的距离为![]() .
.
![]() 试求该抛物线的关系式;
试求该抛物线的关系式;
![]() 若点
若点![]() 在此抛物线上,且点
在此抛物线上,且点![]() 在第一象限,求以点
在第一象限,求以点![]() 、
、![]() 和坐标原点
和坐标原点![]() 为顶点的
为顶点的![]() 面积.
面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com