
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .
.

(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() ,
,![]() ,
,![]() 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称![]() ,
,![]() ,
,![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() ,
,![]() ,
,![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
【答案】(1)B(0,2),![]() ;(2)①点M的坐标为(
;(2)①点M的坐标为(![]() ,0)或M(
,0)或M(![]() ,0);②m=-1或m=
,0);②m=-1或m=![]() 或m=
或m=![]() .
.
【解析】
试题分析:(1) 把点![]() 代入
代入![]() 求得c值,即可得点B的坐标;抛物线
求得c值,即可得点B的坐标;抛物线![]() 经过点
经过点![]() ,即可求得b值,从而求得抛物线的解析式;(2)由
,即可求得b值,从而求得抛物线的解析式;(2)由![]() 轴,M(m,0),可得N(
轴,M(m,0),可得N(![]() ),①分∠NBP=90°和∠BNP =90°两种情况求点M的坐标;②分N为PM的中点、P为NM的中点、M为PN的中点3种情况求m的值.
),①分∠NBP=90°和∠BNP =90°两种情况求点M的坐标;②分N为PM的中点、P为NM的中点、M为PN的中点3种情况求m的值.
试题解析:
(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,解得c=2
,解得c=2
∴B(0,2),
∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,∴b=
,∴b=![]()
∴抛物线的解析式为![]() ;
;
(2)∵![]() 轴,M(m,0),∴N(
轴,M(m,0),∴N(![]() )
)
①有(1)知直线AB的解析式为![]() ,OA=3,OB=2
,OA=3,OB=2
∵在△APM中和△BPN中,∠APM=∠BPN, ∠AMP=90°,
若使△APM中和△BPN相似,则必须∠NBP=90°或∠BNP =90°,
分两种情况讨论如下:
(I)当∠NBP=90°时,过点N作NC![]() 轴于点C,
轴于点C,
则∠NBC+∠BNC=90°,NC=m,
BC=![]()
∵∠NBP=90°,∴∠NBC+∠ABO=90°,
∴∠BNC=∠ABO,
∴Rt△NCB∽ Rt△BOA
∴![]() ,即
,即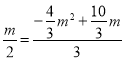 ,解得m=0(舍去)或m=
,解得m=0(舍去)或m=![]()
∴M(![]() ,0);
,0);
(II)当∠BNP=90°时, BN![]() MN,
MN,
∴点N的纵坐标为2,
∴![]()
解得m=0(舍去)或m=![]()
∴M(![]() ,0);
,0);
综上,点M的坐标为(![]() ,0)或M(
,0)或M(![]() ,0);
,0);
②m=-1或m=![]() 或m=
或m=![]() .
.


科目:初中数学 来源: 题型:
【题目】某中学为了创建“最美校园图书屋”,新购买了一批图书,其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元,则下面所列方程中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,在△ABC中,∠BCA=90°,AC=kBC,点D,E分别在边BC,AC上,且AE=kCD,作线段DF⊥DE,且DE=kDF,连接EF交AB于点G.
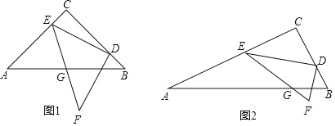
(1)如图1,当k=1时,求证:①∠CED=∠BDF,②AG=GB;
(2)如图2,当k≠1时,猜想![]() 的值,并说明理由;
的值,并说明理由;
(3)当k=2,AE=4BD时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
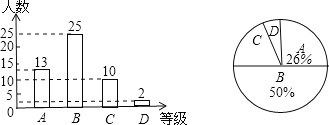
【题目】某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下)
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图中C级所在的扇形圆心角的度数;
(3)该班学生体育测试成绩的中位数落在哪个等级内;
(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
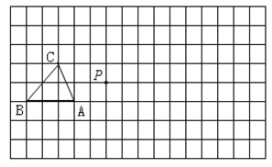
【题目】在下面的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处) .
(1)作出△ABC的中心对称图形△![]() ,A点为对称中心;
,A点为对称中心;
(2)作出△ABC关于点P的位似△A'B'C',且位似比为1:2;
(3)在图中画出以A、B、C为顶点的平行四边形的第四个顶点D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则称这个点为强点.例如,图中过点P分別作x轴,y轴的垂线与坐标轴围成矩形OAPB的周长与面积相等,则点P是强点.
(1)点M(l,2),N(4,4),Q(6,-3)中,是强点的有 ;
(2)若强点P(2a,3)在双曲线![]() 上,求a和b的值.
上,求a和b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,
为常数,![]() )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标;
(2)若点![]() ,
,![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,试比较
,试比较![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,∠ACB=90°,∠BAC=30°,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)当点B于点O重合的时候,求三角板运动的时间;
(2)三角板继续向右运动,当B点和E点重合时,AC与半圆相切于点F,连接EF,如图2所示.
①求证:EF平分∠AEC;
②求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
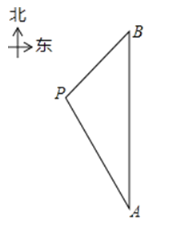
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com