
����Ŀ���������������еĽ�����ʽ֮һ����ĩ����ɫ���о��ֲ�����֯��һ�δӼس�����Ŀ�ĵ�Ϊ�ҵص����л���������ֲ������г��ӳ���1Сʱ��ǡ��һ��Ħ�г��Ӽس����������г����н�·��ǰ���ҵأ������ҵغ�������ԭ·���ؼأ����г�����Ħ�г���ʻ�ٶȾ����ֲ��䣬����Ħ�г���ʻ�ٶ������г�����ʻ�ٶȵ�3������ͼ��ʾ�������г��ӡ�Ħ�г���ص�·��![]() �����г����뿪�ص�ʱ��
�����г����뿪�ص�ʱ��![]() �Ĺ�ϵͼ�������ͼ���ṩ����Ϣ���ش��������⣮
�Ĺ�ϵͼ�������ͼ���ṩ����Ϣ���ش��������⣮
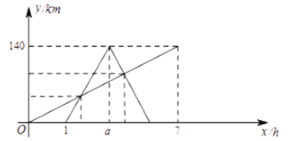
��1��Ħ�г���ʻ���ٶ���__________��![]() ____________��
____________��
��2��������г�����ص�·��![]() �����г����뿪�ص�ʱ��
�����г����뿪�ص�ʱ��![]() �Ĺ�ϵʽ����������г��ӳ�������Сʱ��Ħ�г�������
�Ĺ�ϵʽ����������г��ӳ�������Сʱ��Ħ�г�������
��3��ֱ��д����Ħ�г������г������![]() ʱ����ʱ��Ħ�г����������˶���Сʱ��
ʱ����ʱ��Ħ�г����������˶���Сʱ��
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() �����г��ӳ�����
�����г��ӳ�����![]() Сʱ��
Сʱ��![]() Сʱ�����г�����������3��Ħ�г������г������
Сʱ�����г�����������3��Ħ�г������г������![]() ʱ����ʱ��Ħ�г�����������
ʱ����ʱ��Ħ�г�����������![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��
��������
��1�����ٶ�![]() ·��
·��![]() ʱ�䣬ʱ��
ʱ�䣬ʱ��![]() ·��
·��![]() �ٶȿ���������ۣ�
�ٶȿ���������ۣ�
��2�������г����ٶȾͿ������Ħ�г����ٶȣ����������������г�������![]() Сʱ���������������������⼴�ɣ�
Сʱ���������������������⼴�ɣ�
��3����������ۣ����Ħ�г��ڷ���;�������г����ٴ�����ʱ��ʱ�䣬���ɵó�����ص�·�̣�
�⣺��1�����г�����ʻ���ٶ�Ϊ![]()
��Ħ�г���ʻ���ٶ�Ϊ![]()
![]()
�ʴ�![]() ��
��![]()
��2�������г��ӳ���xСʱ��Ħ�г����������г��ӵĺ�����ϵʽΪ��![]() ��
��
����ͼ��ɵã�![]() ��
��
��![]()
�����г��ӵĺ�����ϵʽΪ��![]() ����
����
���״����� �������![]() �����
�����![]()
��Ħ�г��ڷ����������г����ٴ�����
���������![]() �����
�����![]() ��
��
�����г��ӳ�����![]() Сʱ��
Сʱ��![]() Сʱ�����г���������
Сʱ�����г���������
��3������Ħ�г�����������![]() Сʱ�����г������
Сʱ�����г������![]() ��
��
����![]() ���������г�����Ħ�г�ǰ��ʱ��
���������г�����Ħ�г�ǰ��ʱ��![]()
���![]() ��
��
����Ħ�г������г���ǰ��ʱ��![]() ��
��
���![]() ��
��
��![]() ʱ����Ħ�г����ҵط��أ������г���δ������
ʱ����Ħ�г����ҵط��أ������г���δ������
![]() �����
�����![]() ��
��
��Ħ�г����ҵط��أ������г���������![]() ��
��
���![]() ��
��
��Ħ�г������г������![]() ʱ����ʱ��Ħ�г�����������
ʱ����ʱ��Ħ�г�����������![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
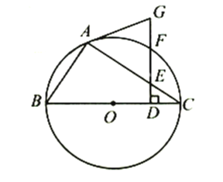
����Ŀ����ͼ����ABC�У���BAC��45������ABC��60����AB��4��D�DZ�BC�ϵ�һ�����㣬��ADΪֱ������O�ֱ�AB��AC�ڵ�E��F������EF���ȵ���СֵΪ�� ��

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
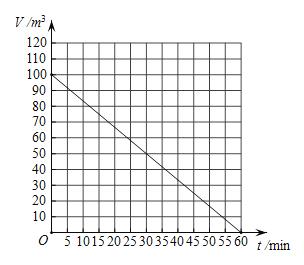
����Ŀ����ͼ������ͼ��ӳ�����ڵ�����V�����ܿ���ʱ��t�ĺ�����ϵ���۲����ͼ�����½�����ȷ����________________��
���������ܿ���ʱ������ӣ������ڵ������ڼ��٣�
�����ܿ���10����ʱ�������ڵ�������80�����ף�
��������������ٴ���40�����ף���ô���������Կ���36���ӣ�
�����ܿ���30���Ӻ����ڵ�����ֻ��ԭ������һ�룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ֽƬABCD�������۵�����ʹ��AB�����ȷ֣�
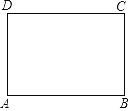
������С����о����̣�
˼������ | Ҫʹ��AB�����ȷ֣����ӱ�DC�Ͽ��ǣ�����Ҫ�۳�DM�� Ҳ����Ҫ�۳�DM�� ��DB��AM�ཻ��Fʱ����Ҫ�۳��Խ����ϵ�DF�� |
�۵�������ʾ��ͼ | ���۳�DB������ֽƬ��ʹD��B�غϣ��õ����ۺ���DB�ཻ�ڵ�E�������۵�ֽƬ��ʹD��B��E�غϣ��õ����ۺ���DB�ֱ��ཻ�ڵ�F��G�� ���۳�AF��CG���ֱ�CD��AB��M��Q�� ����M��ֽƬ��ʹD����MC�ϣ��õ��ۺ�MN�����AB��N��Q���ȷ֣�
|
��1������С����о����̣�˵��AN��NQ��QB��
��2����һ����С�첻ͬ�ķ����۵���ʹ��AB�����ȷ֣���������۵�����������ʾ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ����һ��3��3�����������������½Ǹ�㣨С�����εĶ��㣩A������Ϊ����1��1�������ϽǸ��B������Ϊ����4��4�������ֲ��ڹ����㣨��1��0����ֱ��y����k��x+1������ĸ������ͬ����k��ȡֵ�����ǣ�������

A.![]() B.
B.![]() C.2D.
C.2D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ��
Ϊ��![]() ���ڽ������Σ�
���ڽ������Σ�![]() Ϊ��
Ϊ��![]() ��ֱ�������߶�
��ֱ�������߶�![]() ��ȡ��
��ȡ��![]() ������˵��غϣ�����
������˵��غϣ�����![]() ���ֱ�
���ֱ�![]() ��Բ����
��Բ����![]() ��
��![]() ������
������![]() ����֪
����֪![]() ��
��
��1����֤��![]() Ϊ��
Ϊ��![]() �����ߣ�
�����ߣ�
��2����֪![]() ����գ�
����գ�
�ٵ�![]() __________
__________![]() ʱ���ı���
ʱ���ı���![]() �����Σ�
������
����![]() ����
����![]() __________ʱ��
__________ʱ��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
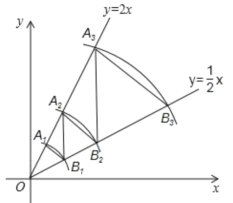
����Ŀ�����κ���![]() �ĺ���ͼ����ͼ����
�ĺ���ͼ����ͼ����![]() λ������ԭ�㣬��
λ������ԭ�㣬��![]() ��
��![]() ����������ϣ���
����������ϣ���![]() �ڶ��κ���
�ڶ��κ���![]() λ�ڵ�һ����ͼ���ϣ�
λ�ڵ�һ����ͼ���ϣ�![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ�Ƕ������������ϵĵ���ֱ�������Σ���
������ֱ�Ƕ������������ϵĵ���ֱ�������Σ���![]() ��б�߳�Ϊ(����)
��б�߳�Ϊ(����)

A.20B.![]() C.22D.
C.22D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ�͡�ѧ���������Ȥ���á������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��
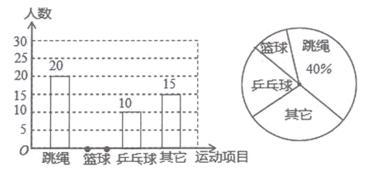
��1������ε����У��������� �ˣ�������ͳ��ͼ�У���ƹ���İٷֱ�Ϊ %�����ѧУ��800��ѧ��������ȫУѧ������ ��ϲ��������Ŀ��
��2���뽫����ͳ��ͼ����������
��3��ѧУ��ϲ������ij�һѧ������ѡ��3��ͬѧ���ֱ����������ֺ��ͳ�����Ȼ������3��ѧ����������ѡ2�˲μ�ѧУ������ӣ������б�������״ͼ�ķ�������������ձ�ѡ�ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ���Ե�
���Ե�![]() ΪԲ�ģ���
ΪԲ�ģ���![]() ��Ϊ�뾶��������ֱ��
��Ϊ�뾶��������ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ΪԲ�ģ���
ΪԲ�ģ���![]() ��Ϊ�뾶��������ֱ��
��Ϊ�뾶��������ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ���Ե�
���Ե�![]() ΪԲ�ģ���
ΪԲ�ģ���![]() ��Ϊ�뾶��������ֱ��
��Ϊ�뾶��������ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() �ύֱ��
�ύֱ��![]() �ڵ�
�ڵ�![]() ���Ե�
���Ե�![]() ΪԲ�ģ���
ΪԲ�ģ���![]() ��Ϊ�뾶�满����ֱ��
��Ϊ�뾶�满����ֱ��![]() �ڵ�
�ڵ�![]() ������������˹��ɽ�����ȥ����
������������˹��ɽ�����ȥ����![]() ������Ϊ__________��
������Ϊ__________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com