
【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形![]() 小长方形纸片长为a,宽为
小长方形纸片长为a,宽为![]() ,请你仔细观察图形,解答下列问题:
,请你仔细观察图形,解答下列问题:
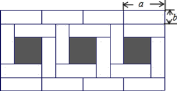
(1)a和b之间的关系满足_____________________.
(2)图中阴影部分的面积与大长方形面积的比值是___________.
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法,请你写出![]() ,
,![]() 与
与![]() 三个代数式之间的等量关系_________________________
三个代数式之间的等量关系_________________________
应用:根据探索中的等量关系,解决如下问题:![]() 求
求![]() 的值
的值
【答案】(1)a=3b;(2)![]() ;(3)(a-b)2=
;(3)(a-b)2=![]() -4
-4![]() ;
;![]() .
.
【解析】
(1)根据小长方形的4个长等于小长方形的3个长和3个宽,列出等式,得出a,b的关系;
(2)根据图形分别表示出阴影部分的面积和大长方形面积,再把(1)的结果代入化简即可;
(3)用两种方法同时表示一个阴影部分的面积,即可得出![]() ,
,![]() 与
与![]() 三个代数式之间的等量关系;利用这个等量关系即可求出
三个代数式之间的等量关系;利用这个等量关系即可求出![]() 的值.
的值.
解:(1)根据图形可得:4a=3a+3b,
解得:a=3b;
故答案为:a=3b;
(2)大长方形的面积是4a(a+3b)=4a×6b=12b×6b=72b2,
阴影部分的面积是3(a-b)2=3(3b-b)2=12b2,
则阴影部分的面积是大长方形面积的![]() ;
;
故答案为:![]() ;
;
(3)根据图形可得一个阴影部分的面积为:(a-b)2或![]() -
-![]() .
.
所以(a-b)2=![]() -
-![]() ;
;
应用:∵![]() ,
,
∴(![]() )2=(
)2=(![]() )2-4xy
)2-4xy
=52-4×![]()
=25-9
=16,
∴![]() =±4.
=±4.
故答案为:(a-b)2=![]() -
-![]() ;±4.
;±4.


科目:初中数学 来源: 题型:
【题目】如图,已知AE⊥BC于E,AF⊥CD于F.
(1)点A到直线BC的距离是线段_______的长;
(2)点D到直线AF的距离是线段_______的长;
(3)线段AF的长表示点A到直线_______距离;
(4)线段CE的长表示点C到直线_______距离;
(5)线段BE的长表示点_______到直线______距离;
(6)线段CF的长表示点_______到直线______距离;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,点E、F分别在直线AB、CD上,∠EPF=90°,∠BEP=∠GEP,则∠1与∠2的数量关系为( )

A. ∠1=∠2B. ∠1=2∠2C. ∠1=3∠2D. ∠1=4∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】刘谦的魔术表演风靡全世界.很多同学非常感兴趣,也学起了魔术.请看刘凯同学把任意有理数对![]() 放逬装有计算装置的魔术盒,会得到一个新的有理数
放逬装有计算装置的魔术盒,会得到一个新的有理数![]() .例如把
.例如把![]() 放入其中,就会得到
放入其中,就会得到![]() ,现将有理数对
,现将有理数对![]() 放入其中,得到的有理数是__________.若将正整数对放入其中,得到的值都为5,则满足条件的所有的正整数对
放入其中,得到的有理数是__________.若将正整数对放入其中,得到的值都为5,则满足条件的所有的正整数对![]() 为__________.
为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生上学的交通方式,现从全校学生中随机抽取了部分学生进行“我上学的交通方式”问卷调查,规定每人必须并且只能在“乘车”、“步行”、“骑车”和“其他”四项中选择一项,并将统计结果绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)在这次调查中,该学校一共抽样调查了 名学生;
(2)补全条形统计图;
(3)若该学校共有1500名学生,试估计该学校学生中选择“步行”方式的人数.
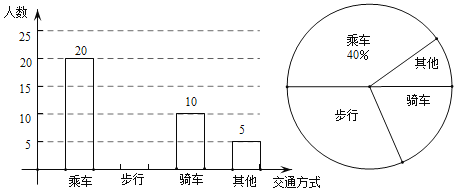
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:

![]() 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
![]() 若点
若点![]() 是点
是点![]() 通过
通过![]() 中的平移变换得到的,求
中的平移变换得到的,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习初中数学的- -个重要工具利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:数轴上点![]() 、点
、点![]() 表示的数为
表示的数为![]() ,则
,则![]() 两点之间的距离
两点之间的距离![]() ,若
,若![]() ,则可简化为;
,则可简化为;![]() 线段
线段![]() 的中点
的中点![]() 表示的数为
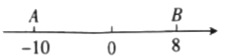
表示的数为![]() 如图,已知数轴上有
如图,已知数轴上有![]() 两点,分别表示的数为
两点,分别表示的数为![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以每秒
以每秒![]() 个单位长度向左匀速运动,设运动时间为
个单位长度向左匀速运动,设运动时间为![]() 秒
秒![]() .
.
(1)运动开始前,![]() 两点的距离为多少个单位长度;线段
两点的距离为多少个单位长度;线段![]() 的中点
的中点![]() 所表示的数为?
所表示的数为?
(2)点![]() 运动
运动![]() 秒后所在位置的点表示的数为 ;点
秒后所在位置的点表示的数为 ;点 ![]() 运动
运动![]() 秒后所在位置的点表示的数为 . (用含
秒后所在位置的点表示的数为 . (用含![]() 的式子表示)
的式子表示)
(3)它们按上述方式运动,![]() 两点经过多少秒会相距
两点经过多少秒会相距![]() 个单位长度?
个单位长度?
(4)若![]() 按上述方式运动,
按上述方式运动, ![]() 两点经过多少秒,线段
两点经过多少秒,线段![]() 的中点
的中点![]() 与原点重合?
与原点重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示-3,点B表示4.
(1)点A与点B之间的距离是 ;
(2)我们知道,在数轴上|a|表示数a所对应的点到原点的距离,你能说明![]() 在数轴上表示的意义吗?
在数轴上表示的意义吗?
(3)在数轴上点P表示的数为x,是否存在这样的点P,使2PA+PB=12?若存在,请求出相应的x;若不存在,请说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com