
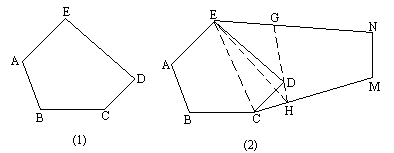
如图,五边形ABCDE是张大爷十年前承包的一块土地的示意图:经过多年开垦荒地,现已变成如图所示的形状,但承包土地与开垦荒地的分界小路(即图中折线CDE还保留着),张大爷想过E点修一条直路,直路修好后,要保持直路左边的土地面积与承包是一样多,右边的与开垦的荒地面积一样多,请你用有关的几何知识,按张大爷的要求进行几何作图,并说明理由.
|
解答:1.连结EC. 2.以D为顶点,DE为边,在△EDC外侧作∠GDE=∠DEC,交EN于G. 3.延长GD交MC于H. 4.连结EH,即EH是所求作的线段. 证明:∵∠GDE=∠DEC,∴GH∥EC,∴S△EDC=S△ECH,∵S五ABCDE=S四ABCE+S△EDC,∴S五ABCDE=S四ABCE+S△ECH=S五ABCHE. |
|
名师导引:要求面积不变且要经过E点作一直线,我们可以先假设这一直线已经作出,观察可以看出,实际上是将△EDC进行等积变换,易想到作平行线以利用同底等高来进行面积转换. 探究点:等积变换的多种方式,积的倍数之间的关系,不等积关系的几何作图. |


科目:初中数学 来源: 题型:
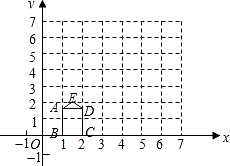 如图,矩形ABCD的长,宽分别为
如图,矩形ABCD的长,宽分别为| 3 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
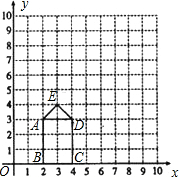 如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com