
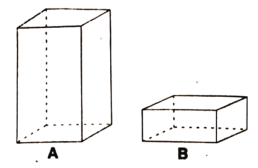
【题目】网购是现在人们常用的购物方式,通常网购的商品为防止损坏会采用盒子进行包装,![]() 均是容积为
均是容积为![]() 立方分米无盖的长方体盒子(如图).
立方分米无盖的长方体盒子(如图).
(1)图中![]() 盒子底面是正方形,
盒子底面是正方形,![]() 盒子底面是长方形,
盒子底面是长方形,![]() 盒子比
盒子比![]() 盒子高6分米,
盒子高6分米,![]() 和
和![]() 两个盒子都选用相同的材料制作成侧面和底面,制作底面的材料1.5元/平方分米,其中
两个盒子都选用相同的材料制作成侧面和底面,制作底面的材料1.5元/平方分米,其中![]() 盒子底面制作费用是
盒子底面制作费用是![]() 盒子底面制作费用的3倍,当
盒子底面制作费用的3倍,当![]() 立方分米时,求
立方分米时,求![]() 盒子的高(温馨提示:要求用列分式方程求解).
盒子的高(温馨提示:要求用列分式方程求解).
(2)在(1)的条件下,已知![]() 盒子侧面制作材料的费用是0.5元/平方分米,求制作一个
盒子侧面制作材料的费用是0.5元/平方分米,求制作一个![]() 盒子的制作费用是多少元?
盒子的制作费用是多少元?
(3)设![]() 的值为(2)中所求的一个
的值为(2)中所求的一个![]() 盒子的制作费用,请分解因式;
盒子的制作费用,请分解因式;![]() .
.
【答案】(1)B盒子的高为3分米;(2)制作一个![]() 盒子的制作费用是240元;(3)
盒子的制作费用是240元;(3)![]() .
.
【解析】
(1)先以“![]() 盒子底面制作费用是
盒子底面制作费用是![]() 盒子底面制作费用的3倍”为等量关系列出分式方程,再求解分式方程,最后检验作答即得.
盒子底面制作费用的3倍”为等量关系列出分式方程,再求解分式方程,最后检验作答即得.
(2)先分别求出A盒子的底面积和四个侧面积,再求出各个面的制作费用之和即得.
(3)先依据(2)写出多项式,再应用十字相乘法因式分解即得.
(1)设B盒子的高为h分米.
由题意得:![]()
解得:![]()
经检验得:![]() 是原分式方程的解.
是原分式方程的解.
答:B盒子的高为3分米.
(2)∵由(1)得B盒子的高为3分米
∴A盒子的高为:![]() (分米)
(分米)
∴A盒子的底面积为:![]() (平方分米)
(平方分米)
∴A盒子的底边长为:![]() (分米)
(分米)
∴A盒子的侧面积为:![]() (平方分米)
(平方分米)
∵底面的材料1.5元/平方分米,侧面制作材料的费用是0.5元/平方分米
∴制作一个![]() 盒子的制作费用是:
盒子的制作费用是:![]() (元)
(元)
答:制作一个![]() 盒子的制作费用是240元.
盒子的制作费用是240元.
(3)∵由(2)得:![]()
∴![]()
∴![]()
![]()
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE.
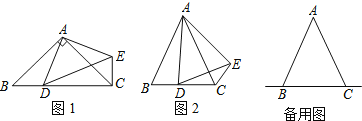
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE= °.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴交于负半轴,给出六个结论:①a>0;②b>0;③c>0;④a+b+c=0;⑤b2﹣4ac>0;⑥2a﹣b>0,其中正确结论序号是_____.
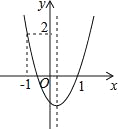
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某移动通信公司推出了如下两种移动电话计费方式.
月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) | |
方式一 |
|
|
|
方式二 |
|
|
|
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费![]() 元,当主叫计时不超过
元,当主叫计时不超过![]() 分钟不再额外收费,超过
分钟不再额外收费,超过![]() 分钟时,超过部分每分钟加收
分钟时,超过部分每分钟加收![]() 元(不足
元(不足![]() 分钟按
分钟按![]() 分钟计算).
分钟计算).
(1)请根据题意完成如表的填空:
月主叫时间 | 月主叫时间 | |
方式一收费/元 | ______________ |
|
方式二收费/元 |
| _______________ |
(2)设某月主叫时间为![]() (分钟),方式一、方式二两种计费方式的费用分别为
(分钟),方式一、方式二两种计费方式的费用分别为![]() (元),
(元),![]() (元),分别写出两种计费方式中主叫时间
(元),分别写出两种计费方式中主叫时间![]() (分钟)与费用为
(分钟)与费用为![]() (元),
(元),![]() (元)的函数关系式;
(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题:
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:因为m2+2mn+2n2﹣6n+9=0,
所以m2+2mn+n2+n2﹣6n+9=0,
所以(m+n)2+(n﹣3)2=0,
所以m+n=0,n﹣3=0,
所以m=﹣3,n=3.
问题(1)若x2+2y2﹣2xy+6y+9=0,求xy的值;
(2)已知a,b,c是△ABC的三边长,满足a2+b2=6a+8b﹣25,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,CE⊥AD于点E,DF⊥BA交BA的延长线于点F.
(1)求证:△ADF∽△DCE;
(2)当AF=2,AD=6,且点E恰为AD中点时,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com