
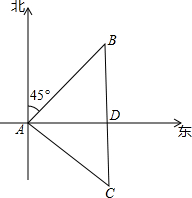
 如图,小明先从A地沿东北方向走100$\sqrt{2}$m,到达B地向正南方向走200m到达C地,
如图,小明先从A地沿东北方向走100$\sqrt{2}$m,到达B地向正南方向走200m到达C地,分析 (1)在直角△ABD中利用三角函数求得AD和BD的长,则CD即可求得,再在直角△ACD中利用勾股定理求解;
(2)利用三角函数求得∠DAC的度数即可确定.
解答 解:(1)△ABD中,∠BAD=45°,
则BD=AB•sin45=100$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=100(m),AD=BD=100(m).
则CD=BC-BD=200-100=100(m),
在△ACD中,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{10{0}^{2}+10{0}^{2}}$=100$\sqrt{2}$(m).
则此时到A的距离是100$\sqrt{2}$m;
(2)tan∠DAC=$\frac{CD}{AD}$=$\frac{100}{100}$=1,则∠DAC=45°.
则小明在A的南偏东45°.
点评 本题考查了方向角和勾股定理以及三角函数,理解解直角三角形的条件是关键.


科目:初中数学 来源: 题型:选择题
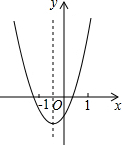 二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )
二次函数y=ax2+bx+c的图象如图所示,下列结论:①abc<0;②2a-b<0;③a+b+c>0;④a-b+c<0;其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
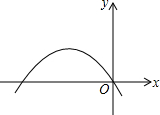 如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).
如图的抛物线是二次函数y=ax2-3x+a2-1的图象,那么a的值是-1,抛物线对称轴为直线x=-$\frac{3}{4}$,顶点是(-$\frac{3}{4}$,$\frac{9}{16}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com