
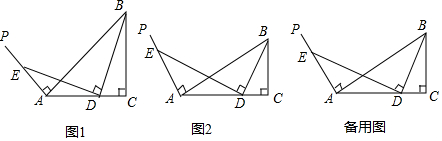
���� ��1����ͼ1���������ߣ�����������ȫ�ȣ�֤����CDG�ǵ���ֱ�������Σ���DG=$\sqrt{2}$CD����DGC=45�㣬��֤����EAD�ա�DGB���ɵý��ۣ�
��2����ͼ2���������ߣ���D��DF��AB����BC��F����֤�á�FDC=30��ã�CF=$\frac{1}{2}$DF��֤����DAE�ס�BFD����$\frac{AD}{BF}=\frac{AE}{FD}$����$\frac{DF}{CF}=\frac{AE}{CD}$���ɵý��ۣ�
��3����ͼ3��ͬ��2���ɵý��ۣ�
��� 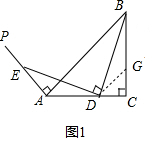 �⣺��1��AE=$\sqrt{2}$CD�������ǣ�
�⣺��1��AE=$\sqrt{2}$CD�������ǣ�
��ͼ1����BC��ȡһ��G��ʹAD=BG������DG��
�ߡ�BAC=45�㣬��ACB=90�㣬
���ACB�ǵ���ֱ�������Σ�
��AC=BC��
��AC-CD=BC-BG��
��CD=CG��
���CDG�ǵ���ֱ�������Σ�
��DG=$\sqrt{2}$CD����DGC=45�㣬
���DGB=135�㣬
��AP��AB��
���BAP=90�㣬
�ߡ�DAE=90��+45��=135�㣬
���DAE=��DGB��
��DE��DB��
���EDB=90�㣬
���EDA+��BDC=90�㣬
�ߡ�BDC+��DBC=90�㣬
���EDA=��DBC��
���EAD�ա�DGB��ASA����
��AE=DG��
��AE=$\sqrt{2}$CD��
�ʴ�Ϊ��AE=$\sqrt{2}$CD��
��2��AE=2CD�������ǣ�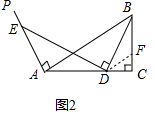
��ͼ2����D��DF��AB����BC��F��
���FDC=��BAC=30�㣬$\frac{AD}{CD}=\frac{BF}{CF}$��
��$\frac{AD}{BF}=\frac{CD}{CF}$��
��AP��AB��DE��BD��
���BAP=��BDE=90�㣬
�ߡ�ADE+��BDE+��BDC=180�㣬
���ADE+��BDC=90�㣬
�ߡ�ACB=90�㣬��FDC=30��
���DBC+��BDC=90�㣬CF=$\frac{1}{2}$DF��
���ADE=��DBC��
�ߡ�DAE=��BAC+��BAP����BFD=��FDC+��ACB��
���DAE=��DBC��
���DAE�ס�BFD��
��$\frac{AD}{BF}=\frac{AE}{FD}$��
��$\frac{CD}{CF}=\frac{AE}{FD}$��
��$\frac{DF}{CF}=\frac{AE}{CD}$��
��$\frac{AE}{CD}$=2����AE=2CD��
��3��CD=AE•sin���������ǣ�
��ͼ3����D��DF��AB����BC��F��
���FDC=��BAC=����$\frac{AD}{CD}=\frac{BF}{CF}$��
��$\frac{AD}{BF}=\frac{CD}{CF}$��
��AP��AB��DE��BD��
���BAP=��BDE=90�㣬
�ߡ�ADE+��BDE+��BDC=180�㣬
���ADE+��BDC=90�㣬
�ߡ�ACB=90�㣬��FDC=����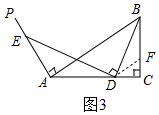
���DBC+��BDC=90�㣬sin��FDC=sin��=$\frac{CF}{DF}$��
���ADE=��DBC��
�ߡ�DAE=��BAC+��BAP����BFD=��FDC+��ACB��
���DAE=��DBC��
���DAE�ס�BFD��
��$\frac{AD}{BF}=\frac{AE}{FD}$��
��$\frac{CD}{CF}=\frac{AE}{FD}$��
��$\frac{CD}{AE}=\frac{CF}{FD}$=sin����
��CD=AE•sin����
���� �����������ε��ۺ��⣬�dz������ͣ�������������ȫ�Ⱥ����Ƶ����ʺ��ж������Ǻ�����ֱ��������30��ǵ����ʡ�����ֱ�������ε����ʺ��ж�������������ȵķ�������������⣬��һ���и����ߵ������ǹؼ��������ı��2�ʺ�3�ʾͱ����֤�������������ƣ����ñ���ʽ������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������㡰����Ϊ��a��b=$\left\{\begin{array}{l}{ab��b��0��}\\{-ab��b��0��}\end{array}\right.$
�������㡰����Ϊ��a��b=$\left\{\begin{array}{l}{ab��b��0��}\\{-ab��b��0��}\end{array}\right.$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪A��-3��n����B��2��-3����һ�κ���y=kx+b�ͷ���������y=$\frac{m}{x}$��ͼ����������㣮
��ͼ����֪A��-3��n����B��2��-3����һ�κ���y=kx+b�ͷ���������y=$\frac{m}{x}$��ͼ����������㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AD�ǵȱ�������BC���ϵĸߣ���ADΪ�����ȱ������Ρ�ADE������BE��
��ͼ��AD�ǵȱ�������BC���ϵĸߣ���ADΪ�����ȱ������Ρ�ADE������BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com