
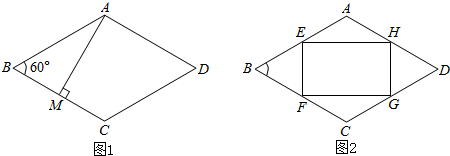
���� ��1������AC��BD��������ԳƵ����ʣ��ɵ�EH��BD��EF��AC����BEFΪ�ȱ������Σ��Ӷ����EF����Rt��AEM�����EM���̶��ó�EH���������ɵó�S��x�ĺ�����ϵʽ��
��2�����ݣ�1���Ĵ𰸣�������ĸ������ε�����������ΪW����ɵó�W����x�Ķ��κ�����ϵʽ�������䷽������ֵ���ɣ�
��� �⣺��1������AC��BD��
��̳Ϊ��Գ�ͼ�Σ�
��EH��BD��EF��AC��
���BEF�ס�BAC��
���ı���ABCD�����Σ�
��AB=BC��
�֡ߡ�ABC=60�㣬
���ABC�ǵȱ������Σ�
ͬ�����õ���BEF�ǵȱ������Σ�
��AB=$\frac{3}{sin60��}$=2$\sqrt{3}$��
��EF=BE=AB-AE=��2$\sqrt{3}$-x��m��
��Rt��AEM�У���AEM=��ABD=30�㣬
��EM=AEcos��AEM=$\frac{\sqrt{3}}{2}$x��
��EH=2EM=$\sqrt{3}$x��
�ʿɵ�S=$\sqrt{3}$x��2$\sqrt{3}$-x��=-$\sqrt{3}$x2+6x��
��2��������ABCD�����Ϊ2$\sqrt{3}$��3=6$\sqrt{3}$��
����EFGH�����Ϊ-$\sqrt{3}$x2+6x��
���ĸ������ε����Ϊ6$\sqrt{3}$+$\sqrt{3}$x2-6x��
���ܷ���ΪW��
��W=200��-$\sqrt{3}$x2+6x��+100��6$\sqrt{3}$+$\sqrt{3}$x2-6x��
=-100$\sqrt{3}$x2+600x+600$\sqrt{3}$
=-100$\sqrt{3}$��x-$\sqrt{3}$��2+900$\sqrt{3}$��
��1��x��2��
�൱x=$\sqrt{3}$ʱ��Wȡ�����ֵ�����ֵΪ900$\sqrt{3}$��
�𣺵�x=$\sqrt{3}$ʱ������������ܷ�����ͣ�����ܷ���900$\sqrt{3}$��
���� ���⿼���˶��κ�����Ӧ�ã�������Ҫ���ݻ�̳Ϊ��Գ�ͼ�Σ��ó�EH��BD��EF��AC���ص����ڷֱ�ó�EF��EH����x�ı���ʽ������Ҫ�����䷽������κ�����ֵ��Ӧ�ã�


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
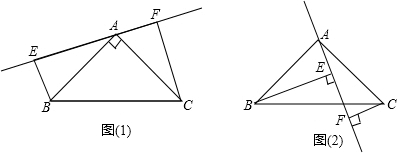
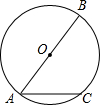 ��ͼ��AB�ǡ�O��ֱ����ACΪ��O���ң���D��ֱ��AB�ϵ�һ�㣬��OA=5cm��AC=8cm����CD�ij��Ȳ������ǣ�������
��ͼ��AB�ǡ�O��ֱ����ACΪ��O���ң���D��ֱ��AB�ϵ�һ�㣬��OA=5cm��AC=8cm����CD�ij��Ȳ������ǣ�������| A�� | 4cm | B�� | 5cm | C�� | 6cm | D�� | 8cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
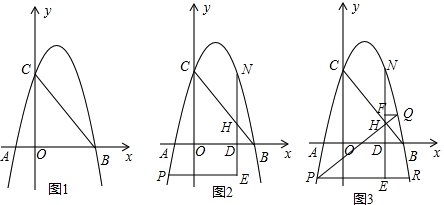
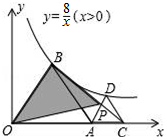 ��ͼ����AOB�͡�ACD��Ϊ�������Σ�����B��D��˫����y=$\frac{8}{x}$��x��0���ϣ��߶�BC��AD���ڵ�P����S��OBP=8��
��ͼ����AOB�͡�ACD��Ϊ�������Σ�����B��D��˫����y=$\frac{8}{x}$��x��0���ϣ��߶�BC��AD���ڵ�P����S��OBP=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ô���ʽ��ʾͼ����Ӱ���ֵ������������x=6ʱ����Ӱ���ֵ����������ȡ3.14��
��ͼ��ʾ���ô���ʽ��ʾͼ����Ӱ���ֵ������������x=6ʱ����Ӱ���ֵ����������ȡ3.14���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com