
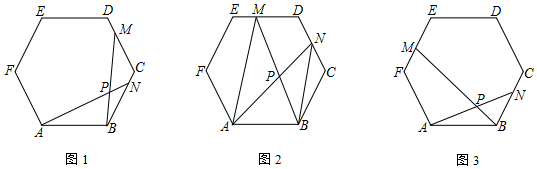
分析 (1)先证明△ABN≌△BCM,得∠ANB=∠BMC,再证明△BPN∽△BCM,列比例式可得结论;
(2)作辅助线,构建等边三角形的三角形的中位线CK,先证明△CDH是等边三角形得:∠HCD=∠CDH=∠H=60°,DC=DH=CH,由△DNG≌△CNK,得KC=DG,DG=$\frac{1}{3}$DH=$\frac{1}{3}$DE,利用四边形MABG是平行四边形,
得MG=AB=ED,所以ME=DG=$\frac{1}{3}$DE,即$\frac{ME}{DE}$=$\frac{1}{3}$;
(3)如图3,作辅助线,构建直角三角形和全等三角形,根据直角三角形30°的性质得:BH=$\frac{1}{2}$,NH=$\frac{\sqrt{3}}{2}$,利用勾股定理求AN=$\sqrt{7}$,证明△ANB≌△GNC,利用EF∥BC和KG∥AB,列比例式可得:$\frac{PG}{AP}=\frac{\frac{14}{3}}{2}$=$\frac{7}{3}$,设PG=7x,AP=3x,根据PG+AP=AG=2$\sqrt{7}$得:7x+3x=2$\sqrt{7}$,可得结论.
解答 (1)证明:在正六边形ABCDEF中,AB=BC,∠ABC=∠BCD=120°,
∵BN=CM,
∴△ABN≌△BCM,
∴∠ANB=∠BMC,
∵∠PBN=∠CBM,
∴△BPN∽△BCM,
∴$\frac{BP}{BC}$=$\frac{BN}{BM}$,
∴BP•BM=BN•BC;
(2)延长BC,ED交于点H,延长BN交DH于点G,取BG的中点K,连接KC,
在正六边形ABCDEF中,∠BCD=∠CDE=120°,
∴∠HCD=∠CDH=60°,
∴∠H=60°,
∴DC=DH=CH,
∵DC=BC,
∴CH=BC,
∵BK=GK,
∴2KC=GH,KC∥DH,
∴∠GDN=∠KCN,
∵CN=DN,∠DNG=∠CNK,
∴△DNG≌△CNK,
∴KC=DG,
∴DG=$\frac{1}{3}$DH=$\frac{1}{3}$DE,
∵MG∥AB,AM∥BG,
∴四边形MABG是平行四边形,
∴MG=AB=ED,
∴ME=DG=$\frac{1}{3}$DE,即$\frac{ME}{DE}$=$\frac{1}{3}$,
(3)如图3,过N作NH⊥AB,交AB的延长线于H,
∵∠ABC=120°,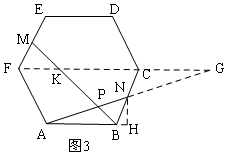
∴∠NBH=60°,
Rt△NBH中,∠BNH=30°,BN=1,
∴BH=$\frac{1}{2}$BN=$\frac{1}{2}$,
∴NH=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
Rt△ANH中,AN=$\sqrt{A{H}^{2}+N{H}^{2}}$=$\sqrt{(2+\frac{1}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{7}$,
连接FC,延长FC与AN交于G,设FC与BM交于K,
易证△ANB≌△GNC,
∴CG=AB=2,AN=NG=$\sqrt{7}$,FC=2AB=4,
∴FG=FC+CG=6,
∵EF∥BC,
∴$\frac{FM}{BC}=\frac{FK}{KC}$,
∴$\frac{1}{2}=\frac{FK}{KC}$,
∵FK+KC=4,
∴FK=$\frac{4}{3}$,KC=$\frac{8}{3}$,KG=$\frac{8}{3}$+2=$\frac{14}{3}$,
∵KG∥AB,
∴$\frac{PG}{AP}=\frac{KG}{AB}$,
∴$\frac{PG}{AP}=\frac{\frac{14}{3}}{2}$=$\frac{7}{3}$,
设PG=7x,AP=3x,
由PG+AP=AG=2$\sqrt{7}$得:7x+3x=2$\sqrt{7}$,
x=$\frac{\sqrt{7}}{5}$,
∴AP=3x=$\frac{3\sqrt{7}}{5}$.
点评 本题是相似三角形的综合题,考查了正六边形的性质、全等三角形和相似三角形的性质和判定、平行四边形的性质和判定、平行线分线段成比例定理等知识,一般情况下,正多边形的题解答都比较麻烦,熟练掌握正多边形的定义及性质是关键,第三问比较复杂,辅助线的作法是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3或-1 | B. | -3或-1 | C. | -3或1 | D. | 3或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,甲地到乙地的路程为260千米,一辆大货车从甲地前往乙地运送物资,行驶2小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过20分钟修好大货车后以原速原路返回甲地,同时大货车以原来1.5倍的速度前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则大货车到达乙地比小汽车返回甲地晚2$\frac{1}{6}$小时.
已知,甲地到乙地的路程为260千米,一辆大货车从甲地前往乙地运送物资,行驶2小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过20分钟修好大货车后以原速原路返回甲地,同时大货车以原来1.5倍的速度前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则大货车到达乙地比小汽车返回甲地晚2$\frac{1}{6}$小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
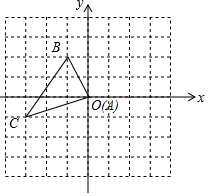 在边长为1的正方形网格中建立平面直角坐标系,△ABC位置如图.
在边长为1的正方形网格中建立平面直角坐标系,△ABC位置如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com