
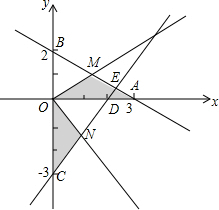
 已知直线y=-$\frac{2}{3}$x+2分别与x轴、y轴相交于A、B两点,过点C(0,-3)作直线AB的垂线交直线AB于点E,交x轴于点D.
已知直线y=-$\frac{2}{3}$x+2分别与x轴、y轴相交于A、B两点,过点C(0,-3)作直线AB的垂线交直线AB于点E,交x轴于点D.分析 (1)由条件可证明△AOB≌△COD,可得OD=OB,可求得D点坐标;
(2)根据△AOM的面积可求得M到x轴的距离,可得M的纵坐标,再代入直线AB的解析式,可求得M的横坐标,可求得M点的坐标,再利用待定系数法可求得直线OM的解析式;
(3)①当三角板两边分别与线段AB、线段CD相交时,可证明△OMA≌△ONC,可得MA=CN,再根据线段的和差可得出结论BM+CN=AB;②当三角板两边分别与线段BA、线段DC的延长线相交时,可证明△OMA≌△ONC,可得到AM=CN,再根据线段的和差可得出结论BM-CN=AB.
解答 解:(1)在y=-$\frac{2}{3}$x+2中,令y=0,可得x=3;令x=0,可得y=2,
∴A(3,0),B(0,2),且C(0,-3),
∴OA=3,OB=2,OC=3,
∵CE⊥AB,
∴∠OBA+∠DCO=∠OBA+∠BAO,
∴∠BAO=∠DCO,
在△AOB和△COD中,
$\left\{\begin{array}{l}{∠BAO=∠DCO}\\{OA=OC}\\{∠AOB=∠COD}\end{array}\right.$
∴△AOB≌△COD(SAS),
∴OD=OB=2,
∴D点坐标为(2,0);
(2)由(1)可知OA=3,
设点M到x轴的距离为h,
∴S△AOM=$\frac{1}{2}$OA•h=$\frac{1}{2}$×3•h=$\frac{3}{2}$,解得h=1,
∴M点的纵坐标为1,
∵M在直线AB上,
∴把y=1代入直线AB解析式可得1=-$\frac{2}{3}$x+2,解得x=$\frac{3}{2}$,
∴M坐标为($\frac{3}{2}$,1),
设直线OM解析式为y=kx,把M坐标代入可得1=$\frac{3}{2}$k,解得k=$\frac{2}{3}$,
∴直线OM的解析式为y=$\frac{2}{3}$x;
(3)①当三角板两边分别与线段AB、线段CD相交时,如图1,
有BM+CN=AB,证明如下: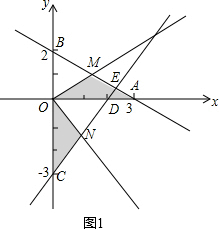
由(1)可知∠MAO=∠NCO,
∵∠MON=∠DOC=90°,
∴∠MOA+∠AON=∠AON+∠NOC,
∴∠MOA=∠NOC,
在△MOA和△NOC中
$\left\{\begin{array}{l}{∠MAO=∠NCO}\\{OA=OC}\\{∠MOA=∠NOC}\end{array}\right.$
∴△MOA≌△NOC(ASA),
∴CN=MA,
∵BM+MA=AB,
∴BM+CN=AB;
②当三角板两边分别与线段BA、线段DC的延长线相交时,如图2,
有BM-CN=AB,证明如下:
由(1)可知∠BAO=∠DCO,
∴∠OAM=∠OCN,
∵∠MON=∠AOC=90°,
∴∠AOM+∠MOC=∠MOC+∠CON,
∴∠AOM=∠CON,
在△AOM和△CON中
$\left\{\begin{array}{l}{∠OAM=∠OCN}\\{OA=OC}\\{∠AOM=∠CON}\end{array}\right.$
∴△AOM≌△CON(ASA),
∴AM=CN,
∵BA+AM=BM,
∴BM-AM=AB,
即BM-CN=AB.
点评 本题主要考查一次函数的综合应用,涉及待定系数法、全等三角形的判定和性质、三角形的面积等知识.在(1)中证明三角形全等是解题的关键,在(2)中求得M点的坐标是解题的关键,在(3)中证明三角形全等得到AM=CN是解题的关键,注意不同图形所得结论也不相同.本题考查知识点较多,综合性较强、难度适中.


科目:初中数学 来源: 题型:解答题
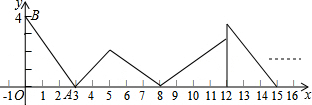
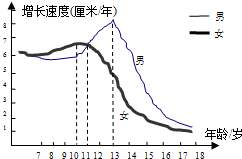 生物学研究表明,在8--17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?
生物学研究表明,在8--17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
根据分式的基本性质,分式 可变形为( )
可变形为( )
A.  B.
B. 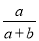 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省咸阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
若(x+m)(x-8)中不含x的一次项,则m的值为( )
A. 8 B. -8 C. 0 D. 8或-8
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
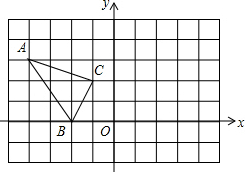 在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.
在平面直角坐标内点A(-4、3),B(-2、0),C(-1,2),将△ABC绕点O顺时针旋转90°后得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
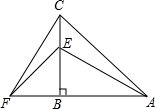 在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.
在△ACF中,CB⊥FA于点B,BE=BF,BA=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com