
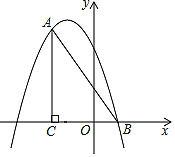
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB=90�㣬OC=2OB��tan��ABC=2����B������Ϊ��1��0����������y=��x2+bx+c����A��B���㣮
��1���������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE=![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2��3x+4����2����P����1��6�����ڴ��ڣ�M����1��3+![]() ����1��3��
����1��3��![]() ����1����1����1��
����1����1����1��![]() ����
����
��������
��1���ȸ�����֪���A�����꣬���ô���ϵ��������κ����Ľ���ʽ��
��2�����ȵ�AB�Ľ���ʽΪ��y=-2x+2������PD��x�ᣬ��P��x��-x2-3x+4������E��x��-2x+2��������PE=![]() DE���з��̿ɵ�P�����ꣻ
DE���з��̿ɵ�P�����ꣻ
�������M�����꣬����������빫ʽ�ɵ�AB��AM��BM�ij����������������ABMΪֱ��������ʱ���ֱ���A��B��MΪֱ�Ƕ���ʱ�����ù��ɶ����з��̿ɵõ�M�����꣮
�⣺��1����B��1��0������OB=1��
��OC=2OB=2����C����2��0����
Rt��ABC��tan��ABC=2��
��![]() �� ��
�� ��![]() �� ��AC=6��
�� ��AC=6��
��A����2��6����
��A����2��6����B��1��0������y=��x2+bx+c�ã�![]() ��
��
��ã�![]() ��
��
�������ߵĽ���ʽΪ��y=��x2��3x+4��
��2���١�A����2��6����B��1��0����
��AB�Ľ���ʽΪ��y=��2x+2��
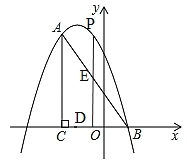
��P��x����x2��3x+4������E��x����2x+2����
��PE=![]() DE��
DE��
�ੁx2��3x+4������2x+2��=![]() ����2x+2����
����2x+2����
��x=-1��1���ᣩ��
��P����1��6����
�ڡ�M��ֱ��PD�ϣ���P����1��6����
��M����1��y����
��B��1��0����A����2��6��
��AM2=����1+2��2+��y��6��2=1+��y��6��2��
BM2=��1+1��2+y2=4+y2��
AB2=��1+2��2+62=45��
�����������
i������AMB=90��ʱ����AM2+BM2=AB2��
��1+/span>��y��6��2+4+y2=45��
��ã�y=3![]() ��
��
��M����1��3+![]() ����1��3��
����1��3��![]() ����
����
ii������ABM=90��ʱ����AB2+BM2=AM2��
��45+4+y2=1+��y��6��2�� ��y=��1��
��M����1����1����
iii������BAM=90��ʱ����AM2+AB2=BM2��
��1+��y��6��2+45=4+y2�� ��y=![]() ��
��
��M����1��![]() ����
����
������������M����������M����1��3+![]() ����1��3��
����1��3��![]() ����1����1����1��
����1����1����1��![]() ����
����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���ȫ�С���ֹ���սոѡ�������ijѧУ�����ˡ���ֹ���սոѣ�������������������Ϊ������ݽ�����. ������ί����������ͬѧ�ijɼ��������������²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ���ṩ����Ϣ������������⣺
������ ������Ϊx�֣� | Ƶ�� | �ٷֱ� |
60��x��70 | 8 | 20% |
70��x��80 | a | 30% |
80��x��90 | 16 | b% |
90��x��100 | 4 | 10% |
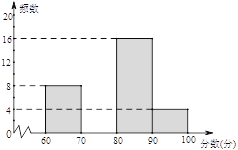
��1�����е�a�� ��b��������������
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3����������ͳ��ͼ�������ɼ��ֲ�������������70��x��80��Ӧ��Բ�ĽǵĶ����� ��
��4�������ɼ�������90�ֵ�4��ͬѧ��������2����ͬѧ��2��Ůͬѧ.ѧУ����4��ͬѧ�������ȡ2��ͬѧ���ܵ���̨���߲ɷã������б�����״ͼ�ķ��������ó鵽һ����ͬѧ��һ��Ůͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+��2m+1��x+m2��2��0��
��1�����÷���������ʵ��������m����С����ֵ��
��2�������̵�����ʵ����Ϊx1��x2���ң�x1��x2��2+m2��21����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
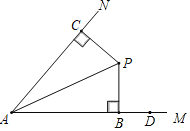
����Ŀ����ͼ����P�ڡ�MAN�ڣ�PAƽ�֡�MAN��PB��AM�ڵ�B��PC��AN�ڵ�C����D������AM�ϵ�B�Ҳ��һ�����㣮
��1��������A��P��D�����Բ����������ͼ�۽�����д������
��2����Բ��AN���ڵ�E����MAN��60����PA��4����AE+AD��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г������̼ƻ�Ͷ��7.1��Ԫ����100��A�ͺ�30��B�����г�������B�ͳ�������A�ͳ����۵�6����60Ԫ��
��1����A��B�����ͺŵ����г����۷ֱ��Ƕ���Ԫ��
��2���������ڸþ������ʽ���ţ�Ͷ�빺�����ʽ���5.86��Ԫ��������������������������䣬��ô�����ܹ���B�ͳ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ�����װ��3����������1��2��4��С�����dz����ֲ�ͬ����״��С��ȫ��ͬ��С���Ӳ��������ȡ��һ��С��������Ϊx��Ȼ��Żز������ȣ��ٴӲ��������ȡ��һ��С��������Ϊy������ȷ���˵�M�����꣨x��y����
��1�����б�����״ͼ�ķ�����ֻѡ����һ�֣�����ʾ����M���п��ܵ����ꣻ
��2�����M��x��y���ں���y��![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�οͳ�������̻ʹ����δ����ڳ����ͼ��꽭�Ľ��㴦A�㣬������������¥����F������Ϊ45������ʱ��ͷ�����Ϸ�146�ĵ�B���мܺ������˻��������ʿ���¥����F������Ϊ31�����δ�����ͷ������ʻ120������ͷC�����¶�i��1��2��б��CD�ߵ���D������ǰ��160��������ʿ¥��E��������ʿ���¥EF�ĸ߶�ԼΪ���������������ȷ��0.1���ο����ݣ�sin31���0.52��cos31���0.87��tan31���0.60��
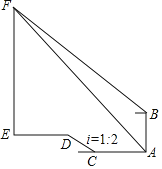
A.301.3��B.322.5��C.350.2��D.418.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
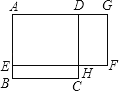
����Ŀ����ͼ��ABCD��һ��߳�Ϊ8�����������ԣ��ֲ����⽫�����Ϊ����AEFG����״�����е�E��AB���ϣ���G��A���ӳ����ϣ�DG��2BE����BE�ij�Ϊx�ף����������AEFG�����Ϊyƽ���ף�
��1����y��x֮��ĺ�����ϵʽ������д�Ա�����ȡֵ��Χ����
��2���������ľ�������AEFG�������ԭ����������ABCD�������ȣ���ʱBE�ij�Ϊ�� ���ף�
��3����xΪ��ֵʱ�����ľ�������AEFG�����������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ı���ABCD��,AB��CD,��B=90��,AB=1,CD=2,BC=3,��PΪBC����һ����,����PAB����PCD������������,��BP�ij�Ϊ _____________
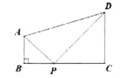
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com