
【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①![]() =3,②
=3,②![]() ,③
,③![]() ,④
,④![]() =5,⑤
=5,⑤![]() =0.
=0.
由上述计算,请写出![]() 的结果(a为任意实数).
的结果(a为任意实数).
(2)利用(1)中的结论,计算下列问题的结果:
①![]() ;
;
②化简:![]() (x<2).
(x<2).
(3)应用:
若![]() =3,求x的取值范围.
=3,求x的取值范围.
【答案】(1)![]() =|a|=
=|a|= ;(2)①π﹣3.14,②2﹣x;(3)x的取值范围是5≤x≤8.
;(2)①π﹣3.14,②2﹣x;(3)x的取值范围是5≤x≤8.
【解析】
(1)将a分为正数、0、负数三种情况得出结果;
(2)①当a=3.14﹣π<0时,根据(1)中的结论可知,得其相反数﹣a,即得π﹣3.14;
②先将被开方数化为完全平方式,再根据公式得结果;
(3)根据(1)式得:![]() =|x﹣5|+|x﹣8|,然后分三种情况讨论:①当x<5时,②当5≤x≤8时,③当x>8时,分别计算,哪一个结果为3,哪一个就是它的取值.
=|x﹣5|+|x﹣8|,然后分三种情况讨论:①当x<5时,②当5≤x≤8时,③当x>8时,分别计算,哪一个结果为3,哪一个就是它的取值.
(1)![]() =|a|=
=|a|= ;
;
(2)①![]() =|3.14﹣π|=π﹣3.14,
=|3.14﹣π|=π﹣3.14,
②![]() (x<2),
(x<2),
=![]() ,
,
=|x﹣2|,
∵x<2,
∴x﹣2<0,
∴![]() =2﹣x;
=2﹣x;
(3)∵![]() =|x﹣5|+|x﹣8|,
=|x﹣5|+|x﹣8|,
①当x<5时,x﹣5<0,x﹣8<0,
所以原式=5﹣x+8﹣x=13﹣2x;
②当5≤x≤8时,x﹣5≥0,x﹣8≤0,
所以原式=x﹣5+8﹣x=3;
③当x>8时,x﹣5>0,x﹣8>0,
所以原式=x﹣5+x﹣8=2x﹣13,
∵![]() =3,
=3,
所以x的取值范围是5≤x≤8.


科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= ![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示). 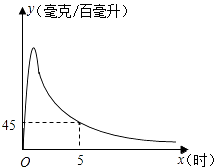
(1)根据上述数学模型计算: ①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当x=5时,y=45,求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论: ①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ![]() ;④3≤n≤4中,
;④3≤n≤4中,
正确的是( )
A.①②
B.③④
C.①④
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,从边长为a的正方形纸片中剪去一个边长为b的小正方形,再沿着线段AB剪开,把剪成的两张纸拼成如图2的等腰梯形, 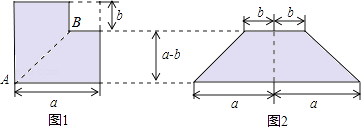
(1)设图1中阴影部分面积为S1 , 图2中阴影部分面积为S2 , 请直接用含a、b的代数式表示S1和S2;
(2)请写出上述过程所揭示的乘法公式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2﹣4ax+3(a≠0)与y轴交于点A,A、B两点关于对称轴对称,直线OB分别与抛物线的对称轴相交于点C.
(1)直接写出对称轴及B点的坐标;
(2)已知直线y2=bx﹣4b+3(b≠0)与抛物线的对称轴相交于点D. ①判断直线y2=bx﹣4b+3(b≠0)是否经过点B,并说明理由;
②若△BDC的面积为1,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有5个黄球,13个黑球和22个红球,它们除颜色外都相同.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于 ![]() ,问至少取出了多少个黑球?
,问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=﹣ ![]() (x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( )
(x<0)的图象上移动,连接OA,作OB⊥OA,并满足∠OAB=30°.在点A的移动过程中,追踪点B形成的图象所对应的函数表达式为( ) 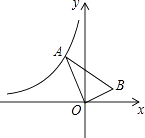
A.y= ![]() (x>0)
(x>0)
B.y= ![]() (x>0)
(x>0)
C.y= ![]() (x>0)
(x>0)
D.y= ![]() (x>0)
(x>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
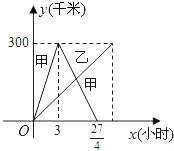
【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)在上述条件下,直接写出它们在行驶过程中相遇时的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com