
【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,且每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两型设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元,预计二期工程完成后每月将产生不少于1300吨污水.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)请你求出用于二期工程的污水处理设备的所有购买方案;
(3)若两种设备的使用年限都为10年,请你说明在(2)的所有方案中,哪种购买方案的总费用最少?(总费用=设备购买费+各种维护费和电费)
【答案】(1)设一台甲型设备的价格为x万元,由题![]() ,解得x=12,∵ 12×75%=9 ,∴ 一台甲型设备的价格为12万元,一台乙型设备的价格是9万元
,解得x=12,∵ 12×75%=9 ,∴ 一台甲型设备的价格为12万元,一台乙型设备的价格是9万元
设二期工程中,购买甲型设备a台,
由题意有![]() ,解得:
,解得:![]()
由题意a为正整数,∴a=1,2,3,4 ∴所有购买方案有四种,分别为
方案一:甲型1台,乙型7台; 方案二:甲型2台,乙型6台
方案三:甲型3台,乙型5台; 方案四:甲型4台,乙型4台
(3)设二期工程10年用于治理污水的总费用为W万元
![]() 化简得:
化简得: ![]() -2a+192,
-2a+192,
∵W随a的增大而减少 ∴当a=4时, W最小(逐一验算也可)
∴按方案四甲型购买4台,乙型购买4台的总费用最少.
【解析】(1)由题中提炼出的1个等量关系,购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%,即可列方程求出;
(2)根据题意列出不等方程组,再解出未知量的取值范围;
(3)首先根据已知得出W与x的函数关系,再利用一次函数的增减性进行分析的得出答案即可.


科目:初中数学 来源: 题型:
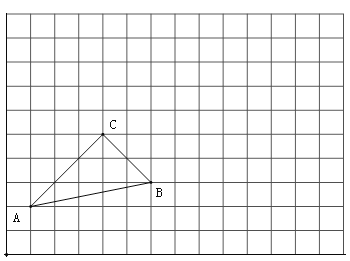
【题目】如图,△ABC是格点三角形(各顶点是网格线的交点), 每个小方格都是边长为1个单位长度的小正方形.
(1)将△ABC向右平移6个单位长度,画出平移后的△A1B1C1.
(2)将平移后的△A1B1C1绕点B1顺时针旋转90°,画出旋转后的△A2B1C2.
(3)将△ABC沿直线BC翻折,画出翻折后的△A3BC.
(4)试问△ABC能否经过一次旋转后与△A2B1C2重合,若能,请在图中用字母O表示旋转中心并写出旋转角的大小;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(m+n)x+n(m<0)的图象与y轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
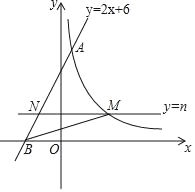
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)观察图象,直接写出当x>0时不等式2x+6﹣![]() <0的解集;
<0的解集;
(3)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去图书批发市场购买某种图书,第一次用1200元购书若干本,并按该书定价7元出售,很快售完.由于该书畅销,第二次购书时,每本书的批发价已比第一次提高了20%,他用1500元所购该书的数量比第一次多10本,当按定价售出200本时,出现滞销,便以定价的4折售完剩余的书.
(1)第一次购书的进价是多少元?
(2)试问该老板这两次售书总体上是赔钱了,还是赚钱了(不考虑其他因素)?若赔钱,赔多少;若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
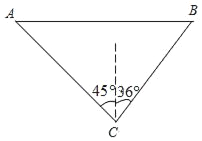
【题目】如图,某湖心岛上有一亭子A,在亭子A的正东方向上的湖边有一棵树B,在这个湖心岛的湖边C处测得亭子A在北偏西45°方向上,测得树B在北偏东36°方向上,又测得B、C之间的距离等于200米,求A、B之间的距离
(结果精确到1米).(参考数据:![]() ≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0. 727,cot36°≈1.376)
≈1.414,sin36°≈0.588,cos36°≈0.809,tan36°≈0. 727,cot36°≈1.376)
查看答案和解析>>
科目:初中数学 来源: 题型:
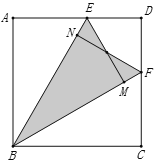
【题目】如图,正方形ABCD的边长为![]() ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
③连接FC.
(2)猜想与证明:猜想四边形ABCF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,……滿足下列条件:a1=0,a2=-│a1+1│,a3=-│a2+2│,a4=-│a3+3│,·……,依次类推,则a2017的值为 ( )
A.-1007B.-1008C.-1009D.-2016
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com