
【题目】已知,如图△ABC中,∠ABC=45°,AB=BC,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F.H是BC边的中点,连接DH与BE相交于点G,

(1)求证BF=AC;
(2)求证CE=![]() BF.
BF.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等腰直角三角形的性质得到BD=CD,证明△BDF≌△CDA,根据全等三角形的性质即可得到BF=AC;
(2)证明△ABE≌△CBE,根据全等三角形的性质得到![]() ,等量代换得到BF=2CE;
,等量代换得到BF=2CE;
证明:(1)∵∠ABC=45°,CD⊥AB于D,
∴△BCD是等腰直角三角形,H是BC边的中点,
∴BD=CD,
∵CD⊥AB于D,BE⊥AC于E,
∴∠DBF+∠A=90°,∠ACD+∠A=90°,
∴∠DBF=∠ACD,
在△BDF与△CDA中,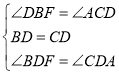 ,
,
∴△BDF≌△CDA(ASA),
∴BF=AC;
(2)∵BE平分∠ABC,且BE⊥AC于E,
∴∠ABE=∠CBE,∠AEB=∠CEB=90°,
∴在△ABE与△CBE中,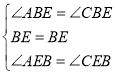
∴△ABE≌△CBE(ASA),
![]()
∴BF=2CE,
即![]() .
.


科目:初中数学 来源: 题型:
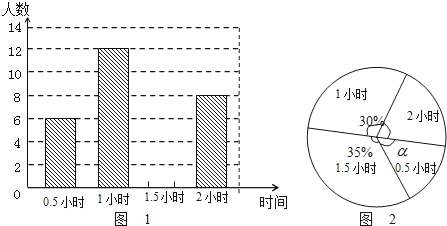
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
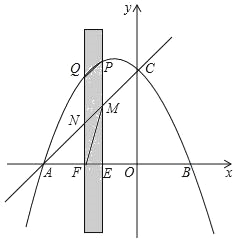
【题目】如图,抛物线y═﹣![]() x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B的坐标为(3,0),点C的坐标为(0,5).有一宽度为1,长度足够长的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B的坐标为(3,0),点C的坐标为(0,5).有一宽度为1,长度足够长的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求抛物线的解析式及点A的坐标;
(2)当点M和N都在线段AC上时,连接MF,如果sin∠AMF=![]() ,求点Q的坐标;
,求点Q的坐标;
(3)在矩形的平移过程中,是否存在以点P,Q,M,N为顶点的四边形是平行四边形,若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=10,∠C=90°,点O在AC边上,且CO=2,点P在BC边上,连接OP绕点O逆时针旋转90°,使得点P落在AB边上的点D处,则CP的长是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC,



(1)求C点的坐标;
(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OPDE的值;
(3)如图3,已知点F坐标为(2,2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①mn为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:

①A、B之间的距离为1200m; ②乙行走的速度是甲的1.5倍;③ b=960; ④ a=34.
以上结论正确的有( )
A. ①② B. ①②③ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
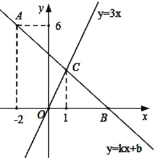
(1)求k、b的值;
(2)请直接写出不等式kx+b>3x中x的范围.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y﹣3与3x+2正比例,且x=2时,y=5
(1)求y与x之间的函数关系式,并指出它是什么函数;
(2)点(4,6)是否在这个函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com