
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?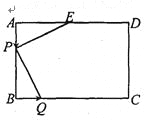
【答案】(1)见详解;(2)S=![]()
![]() t+6;(3)
t+6;(3)![]()
【解析】
(1)本题很容易证明△AEP≌△BPQ,这样可得出∠AEP=∠BPQ,因为∠AEP+∠APE=90°,可得出∠BPQ+∠APE=90°,这即可判断出结论.
(2)可分别用t表示出AP、BQ、BP、CQ的长度,然后用矩形的面积减去△APE、△BPQ及梯形EDCQ的面积即可得出△PEQ的面积为Scm2.
(3)设Q运动的速度为xcm/s,则根据△AEP与△BQP得出AP=BP、AE=BQ或AP=BQ,AE=BP,从而可列出方程组,解出即可得出答案.
(1)∵长方形ABCD,
∴∠A=∠B=90°,
∵点E为AD的中点,AD=6cm,
∴AE=3cm,
又∵P和Q的速度相等可得出AP=BQ=1cm,BP=3,
∴AE=BP,
在△AEP和△BQP中,
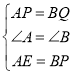
∴△AEP≌△BPQ,
∴∠AEP=∠BPQ,
又∵∠AEP+∠APE=90°,
故可得出∠BPQ+∠APE=90°,即∠EPQ=90°,
即EP⊥PQ.
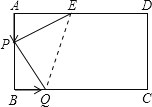
(2)连接QE,由题意得:AP=BQ=t,BP=4t,CQ=6t,
SPEQ=SABCDSBPQSEDCQSAPE
=AD×AB![]() AE×AP
AE×AP![]() BP×BQ
BP×BQ![]() (DE+CQ)×CD
(DE+CQ)×CD
=24![]() ×3t
×3t![]() t(4t)
t(4t) ![]() ×4(3+6t)
×4(3+6t)
=![]()
![]() t+6,
t+6,
(3)设点Q的运动速度为xcm/s,
①经过y秒后,△AEP≌△BQP,则AP=BP,AE=BQ,
∴![]() ,
,
解得:![]() ,
,
即点Q的运动速度为![]() cm/s时能使两三角形全等.
cm/s时能使两三角形全等.
②经过y秒后,△AEP≌△BPQ,则AP=BQ,AE=BP,
∴![]()
解得:![]() (舍去).
(舍去).
综上所述,点Q的运动速度为![]() cm/s时能使两三角形全等.
cm/s时能使两三角形全等.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】某校八年级(1)班要从班级里数学成绩较优秀的甲、乙两位学生中选拔一人参加“全国初中数学联赛”,为此,数学老师对两位同学进行了辅导,并在辅导期间测验了6次,测验成绩如下表(单位:分):
次数,1, 2, 3, 4, 5, 6
甲:79,78,84,81,83,75
乙:83,77,80,85,80,75
利用表中数据,解答下列问题:
(1)计算甲、乙测验成绩的平均数.
(2)写出甲、乙测验成绩的中位数.
(3)计算甲、乙测验成绩的方差.(结果保留小数点后两位)
(4)根据以上信息,你认为老师应该派甲、乙哪名学生参赛?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
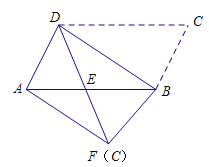
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
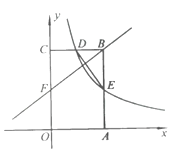
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y=![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)直接写出k的值及点E的坐标;
(2)若点F是OC边上一点,且FB⊥DE,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 上有一点
上有一点![]() ,过
,过![]() 作射线
作射线![]() ,嘉琪将一直角三角板的直角顶点与
,嘉琪将一直角三角板的直角顶点与![]() 重合.
重合.

(1)嘉琪把三角板![]() 如图1放置,若
如图1放置,若![]() ,则
,则![]() ,
,![]() ;
;
(2)嘉琪将直角三角板绕![]() 点顺时针旋转一定角度后如图2,使
点顺时针旋转一定角度后如图2,使![]() 平分
平分![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一假期某学校计划组织385名师生租车旅游,现知道出租公司有42座和60座客车,每辆42座比每辆60座客车租金便宜140元,租3辆42座和2每辆60座客车租金共计1880元
(1) 求两种车租金每辆各多少元?
(2) 若学校同时租用这两种客车8辆(可以坐不满),总租金不超过3200元,有几种租车方案?请选择最节省的租车方案
查看答案和解析>>
科目:初中数学 来源: 题型:
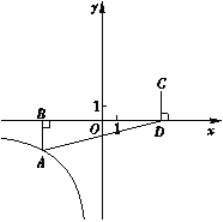
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形 纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③).


图②矩形(正方形)
 ,
,
分别在图①、图②、图③中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形.
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙.
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com