
【题目】已知反比例函数的图象经过点A(2,6).
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于哪些象限?y随x的增大如何变化?
(3)点B(3,4),C(5,2),D(![]() ,
,![]() )是否在这个函数图象上?为什么?
)是否在这个函数图象上?为什么?
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
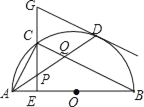
【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
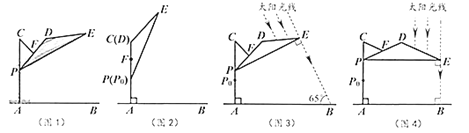
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种植某产品种蜜柚![]() 已知该蜜柚的成本价为8元
已知该蜜柚的成本价为8元![]() 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量![]() 千克
千克![]() 与销售单价
与销售单价![]() 元
元![]() 千克
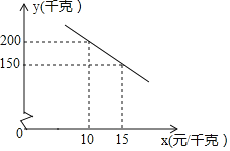
千克![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求y与x的函数关系式,并写出x的取值范围;
求y与x的函数关系式,并写出x的取值范围;
![]() 当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
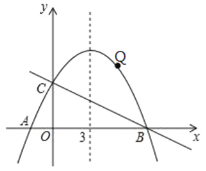
【题目】如图,已知抛物线y=ax+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)求出A点的坐标、B点坐标;
(2)求出直线BC的解析式;
(3)点Q是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点Q,使△QBC的面积最大.若存在,请求出△QBC的最大面积,若不存在,试说明理由;
(4)若E在x轴上,点F在抛物线上,以A、C、E、F为顶点的四边形是平行四边形时,请直接写出点E的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】放学后,小刚和同学边聊边往家走,突然想起今天是妈妈的生日,赶紧加快速度,跑步回家.小刚离家的距离s(m)和放学后的时间t(min)之间的关系如图所示,给出下列结论:①小刚边走边聊阶段的行走速度是125m/min;②小刚家离学校的距离是1000m;③小刚回到家时已放学10min;④小刚从学校回到家的平均速度是100m/min;其中正确的个数为是( )
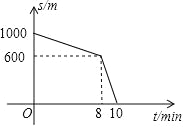
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com