
【题目】如图,点D为△ABC的AB边上的中点,点E为AD的中点,△ADC为正三角形,给出下列结论,①CB=2CE,②tan∠B=![]() ,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是____(填写正确结论的序号).
,③∠ECD=∠DCB,④若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,则d12+d22的最小值是3.其中正确的结论是____(填写正确结论的序号).
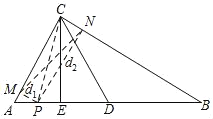
【答案】①③④
【解析】
根据中点的性质得到AD=BD,根据等边三角形的性质得到AD=CD,∠ADC=∠ACD=60°,CE⊥AB,∠DCE=30°,根据等量代换有CD=BD,根据等腰三角形的性质得到∠B=∠DCB=30°,即可判断①②③,根据勾股定理可知d12+d22=MN2=CP2,根据垂线段最短,则当CP⊥AB时,d12+d22的值最小,即可判断④.
∵D是AB中点
∴AD=BD
∵△ACD是等边三角形,E是AD中点
∴AD=CD,∠ADC=∠ACD =60°,CE⊥AB,∠DCE=30°
∴CD=BD
∴∠B=∠DCB=30°,且∠DCE=30°,CE⊥AB
∴∠ECD=∠DCB,BC=2CE,tan∠B=![]()
故①③正确,②错误
∵∠DCB=30°,∠ACD=60°
∴∠ACB=90°
若AC=2,点P是AB上一动点,点P到AC、BC边的距离分别为d1,d2,
∴四边形PMCN是矩形
∴MN=CP
∵d12+d22=MN2=CP2
∴当CP为最小值,d12+d22的值最小
∴根据垂线段最短,则当CP⊥AB时,d12+d22的值最小
此时:∠CAB=60°,AC=2,CP⊥AB
∴CP=![]() ,
,
∴d12+d22=MN2=CP2=3
即d12+d22的最小值为3
故④正确
故答案为①③④


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
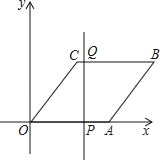
【题目】如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(8,4),点C的坐标为(3,4),连接AB、BC、OC
(1)求证四边形OABC是菱形;
(2)直线l过点C且与y轴平行,将直线l沿x轴正方向平移,平移后的直线交x轴于点P.
①当OP:PA=3:2时,求点P的坐标;
②点Q在直线1上,在直线l平移过程中,当△COQ是等腰直角三角形时,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、价价各几何?“其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问:合伙人数、羊价各是多少?设合伙人数为![]() 人,羊价为
人,羊价为![]() 钱,根据题意,可列方程组( )
钱,根据题意,可列方程组( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
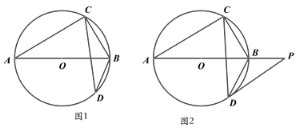
【题目】已知AB是⊙O的的直径,弦CD与AB相交,∠BCD=25°。
(1)如图1,求∠ABD的大小;
(2)如图2,过点D作O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,D是AB边的中点,E是AC边上一点,联结DE,过点D作
,D是AB边的中点,E是AC边上一点,联结DE,过点D作![]() 交BC边于点F,联结EF.
交BC边于点F,联结EF.
(1)如图1,当![]() 时,求EF的长;
时,求EF的长;
(2)如图2,当点E在AC边上移动时, ![]() 的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出
的正切值是否会发生变化,如果变化请说出变化情况;如果保持不变,请求出![]() 的正切值;
的正切值;
(3)如图3,联结CD交EF于点Q,当![]() 是等腰三角形时,请直接写出BF的长.
是等腰三角形时,请直接写出BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
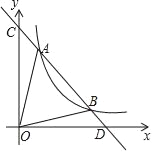
【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
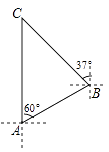
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
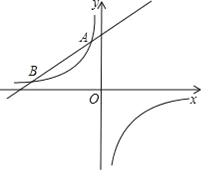
【题目】如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=﹣8x-1的函数交于A(﹣2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com