为了解居民用水情况，晓娜在某小区随机抽查了10户家庭的月用水量，结果如下表：
| 月用水量（吨） | 5 | 6 | 7 | 8 | 9 | 10 |
| 户数 | 1 | 1 | 2 | 2 | 3 | 1 |
则这10户家庭的月用水量的平均数和众数分别是
A．7.8，9 B．7.8
，3 C．4.5，9 D．4.5，3
阅读快车系列答案科目：初中数学 来源： 题型：
如图，平行四边形纸片ABCD，CD＝5，BC＝2，∠A＝60°，将纸片折叠，使点A落在射线AD上（记为点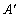
），折痕与AB交于点P，设AP的长为x，折叠后纸片重叠部分的面积为y，可以表示y与x之间关系的大致图象是（ ）
| |
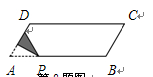
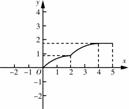
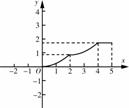
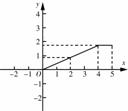
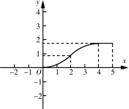
B．
C． D． 查看答案和解析>>
科目：初中数学 来源： 题型：
在平面直角坐标系xOy中，已知 A(-2，0)，B(2，0)，AC⊥AB于点A，AC=2，BD⊥AB于点B，BD=6，以AB为直径的半圆O上有一动点P（不与A、B两点重合），连接PD、PC，我们把由五条线段AB、BD、DP、PC、CA所组成的封闭图形ABDPC叫做点P的关联图形，如图1所示.
（1）如图2，当P运动到半圆O与y轴的交点位置时，求点P的关联图形的面积.
（2）如图3，连接CD、OC、OD,判断△OCD的形状，并加以证明.
（3）当点P运动到什么位置时，点P的关联图形的面积最大，简要说明理由，并求面积的最大值.
 | |||
 | |||
查看答案和解析>>
科目：初中数学 来源： 题型：
在平面直角坐标系xOy中，一次函数
的图象与反比例函数
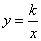的图象的一
个交点为A（1，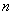
）.
（1）求反比例函数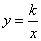的解析式；
（2）若P是坐标轴上一点（P不与O重合），且满足
，直接写出点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，正方形ABCD的边长是2，M是AD的中点．
点E从点A出发，沿AB运动到
点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．
（1）设AE=x时，△EGF的面积为y．求y关于x的函数关系式，
并写出自变量x的取值范围；
（2）P是MG的中点，求点P运动路线的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
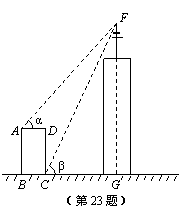如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α＝48°，∠β＝65°，矩形建筑物宽度AD＝20 m，高度DC＝33 m．计算该信号发射塔顶端到地面的高度FG（结果精确到1m）．（参考数据：sin48°≈0.7，cos48°≈0.7，tan48°≈1.1，sin65°≈0.9，cos65°≈0.4，tan65°≈2.1）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=_______________．
，求代数式
的值.
有意义的x的取值范围是 ．